题目内容
4.| 计算: (1)28+(-72) | (2)0+(-5) | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) |
| (4)(-3)-(-5) | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ | (6)(-8)+(-5)-(+5) |
| (7)-37-40+3-22 | (7)$(({-4})×({-\frac{3}{4}})×2$ | (8)(-5)×(-4)×3×(-2) |
| (9)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ | (10)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ | (11)9$\frac{15}{16}×({-8})$ |
| (12)100÷$\frac{1}{8}×({-8})$ | (13)$1÷({-\frac{2}{7}})×\frac{1}{7}$ | (14)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$. |
分析 根据有理数的加减乘除的法则进行计算即可.
解答 解:
| (1)28+(-72) =-(72-28) =-44 | (2)0+(-5) =-5 | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) =-($\frac{1}{5}-\frac{1}{6}$) =-$\frac{1}{30}$ |
| (4)(-3)-(-5) =(-3)+5 =2 | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ =($-3\frac{1}{2}$)+($-5\frac{1}{4}$) =-$8\frac{3}{4}$ | (6)(-8)+(-5)-(+5) =(-8)+(-5)+(-5) =-18 |
| (7)-37-40+3-22 =(-37)+(-40)+3+(-22) =-96 | (8)$(({-4})×({-\frac{3}{4}})×2$ =3×2 =6 | (9)(-5)×(-4)×3×(-2) =-5×4×3×2 =-120 |
| (10)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ =12×4×$\frac{3}{8}$ =18 | (11)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ =$(\frac{1}{3}-\frac{5}{6}+\frac{7}{9})×18$ =6-15+14 =5 | (12)9$\frac{15}{16}×({-8})$ =-$\frac{159}{16}$×8 =$-\frac{159}{2}$ |
| (13)100÷$\frac{1}{8}×({-8})$ =-100×8×8 =-6400 | (14)$1÷({-\frac{2}{7}})×\frac{1}{7}$ =-1×$\frac{7}{2}×\frac{1}{7}$ =-$\frac{1}{2}$ | (15)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$ =-$\frac{1}{2}×\frac{4}{15}×\frac{3}{2}$ =-$\frac{1}{5}$ |
点评 本题考查有理数的混合运算,关键是明确有理数的加减乘除的法则.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.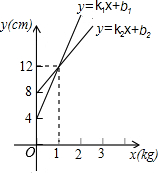 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
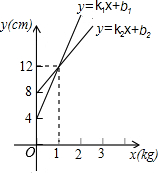 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
12.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. |  +4.5 | B. |  -1.5 | C. |  -0.4 | D. |  +0.6 |
14.一个五次六项式加上一个六次七项式等于几次几项式( )
| A. | 十一次十三项式 | B. | 六次十三项式 | C. | 六次多项式 | D. | 六次整式 |
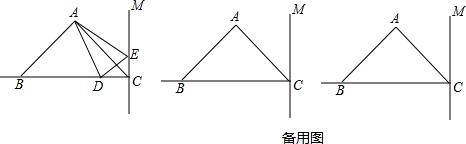
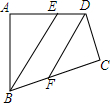 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?