题目内容
1.操作:小明准备制作一个制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计: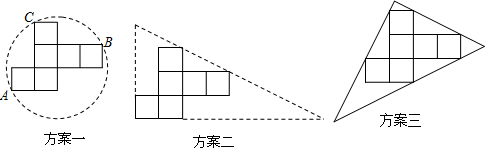
说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
方案三中的每条边均过其中两个正方形的顶点.
纸片利用率=$\frac{纸片被利用的面积}{纸片的总面积}$×100%
发现:(1)小明发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率约为38.2%,你知道怎么算的吗?请你写出他的计算过程;
(3)对于方案二纸片的利用率,小明认为关键的是要求出此直角三角形的两直角边的长,你是这样想的吗?请你选用合适的方法求出方案二纸片的利用率.(结果精确到0.1%)
探究:
(4)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率:49.9%.(结果精确到0.1%)
分析 (1)连接AC、BC、AB,据每个小正方形的边长为1,可以证得∠ACB=90°,故问题可求.
(2)求得圆的半径后可以求得纸片的面积,从而利用展开图的面积除以总面积即可求得利用率;
(3)如图,作辅助线,利用三角形全等和三角形相似对应边成比例,可以分别求得直角三角形的两个直角边的长度,于是问题可求;
(4)利用方案(3)的方法,分析求解即可求得答案.
解答 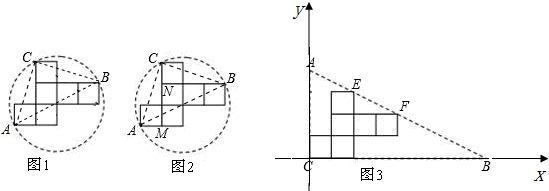 解:(1)小明的这个发现正确.
解:(1)小明的这个发现正确.
理由:如图1:连接AC、BC、AB,
∵AC=BC=$\sqrt{10}$,AB=$\sqrt{20}$;
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴AB为该圆的直径.
解法二:如图2:连接AC、BC、AB.
易证△AMC≌△BNC,
∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,
∴∠BCN+∠ACM=90°,即∠ACB=90°,
∴AB为该圆的直径.…(3分)
(2)∵由题意知:AB=2$\sqrt{{1}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴圆的半径为$\sqrt{5}$,∴圆的面积为5π,
∵展开图的面积为6,
∴利用率=$\frac{展开图的面积}{纸板的总面积}$×100%=$\frac{6}{5π}$×100%=38.2%;
(3)如图3:建立平面直角坐标系,可得E(2,3)、F(4,2)得直线解析式为y=-$\frac{1}{2}$x+4,
∴A(0,4)B(8,0)
∴AC=4 BC=8.
∴S△ACB=16.
∴该方案纸片利用率=$\frac{展开图的面积}{纸板的总面积}$×100%=$\frac{6}{16}$×100%=37.5%.
(4)探究:过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,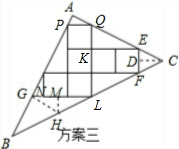
设AP=a,
∵PQ∥EK,
易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴AP:AQ=QK:EK=1:2,
∴AQ=2a,PQ=$\sqrt{5}$a,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=$\frac{5}{2}$a,
则PG=5a+$\frac{5}{2}$a=$\frac{15}{2}$a,GL=$\frac{5}{2}\sqrt{5}$a,
∴GH=$\frac{25}{8}$a,
∵$\frac{GH}{2a+5a+\frac{5}{2}a}$=$\frac{GB}{GB+\frac{15}{2}a+a}$,
解得:GB=$\frac{25}{6}$a,
∴AB=$\frac{38}{3}$a,AC=$\frac{19}{2}$a,
∴S△ABC=$\frac{1}{2}$×AB×AC=$\frac{361}{6}$a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=$\frac{展开图的面积}{纸板的总面积}$×100%=$\frac{180}{361}$×100%=49.86%≈49.9%.
点评 此题考查了圆周角的性质,相似三角形与全等三角形的判定与性质,勾股定理的逆定理等知识.此题综合性很强,难度较大,解题时要注意数形结合思想的应用.

| A. |  +4.5 | B. |  -1.5 | C. |  -0.4 | D. |  +0.6 |
| A. | 3 | B. | 2 | C. | -1 | D. | 0 |
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有一个实数根 |
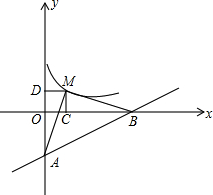 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.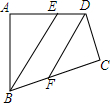 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?