题目内容
20. △ABC中,AB=AC,AD是△ABC的中线,BF垂直AC于F交AD于E,连接CE交AB于点G,求证:CG⊥AB.
△ABC中,AB=AC,AD是△ABC的中线,BF垂直AC于F交AD于E,连接CE交AB于点G,求证:CG⊥AB.
分析 根据等腰三角形性质求出AD⊥BC,∠FCB=∠GBC,求出EB=EC,∠EDC=∠EDB=90°,根据ASA推出△FBC≌△GCB,根据全等三角形的性质得出∠BFC=∠BGC即可.
解答 证明:∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴EB=EC,∠EDC=∠EDB=90°,
∴∠GCB=∠FBC,
∵AB=AC,
∴∠FCB=∠GBC,
在△FBC和△GCB中,
$\left\{\begin{array}{l}{∠FCB=∠GBC}\\{BC=BC}\\{∠FBC=∠GCB}\end{array}\right.$,
∴△FBC≌△GCB(ASA),
∴∠BFC=∠BGC,
∵BF⊥AC,
∴∠BFC=90°,
∴∠BGC=90°,
∴CG⊥AB.
点评 本题考查了等腰三角形的性质,全等三角形的性质和判定的应用,解此题的关键是求出△FBC≌△GCB,题目比较好,难度适中.

练习册系列答案
相关题目
15.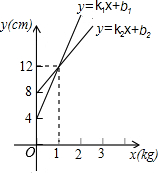 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
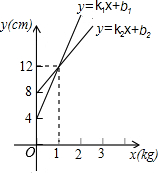 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
12.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. |  +4.5 | B. |  -1.5 | C. |  -0.4 | D. |  +0.6 |
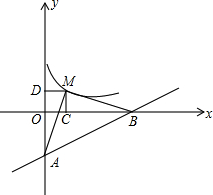 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.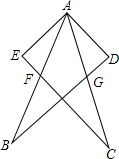 已知:如图,∠EAB=∠DAC,∠B=∠C,AB=AC.求证:EF=DG.
已知:如图,∠EAB=∠DAC,∠B=∠C,AB=AC.求证:EF=DG.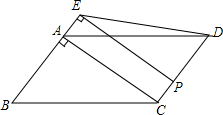 如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).
如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).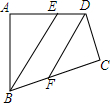 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?