题目内容
19.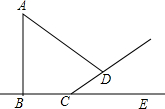 九(1)班的同学到郊外展开活动,在土坡旁看见一棵古树,班上同学很想知道古树AB的高.小王拿尺子量得古树在地面上的影子BC=8米,在斜坡上面的影子CD=6米,测得斜坡CD与地面成∠DCE=30°,同一时刻小李量的1.5米的旗杆在地上面的影子长是2米.请你根据以上数据算出古树的高.
九(1)班的同学到郊外展开活动,在土坡旁看见一棵古树,班上同学很想知道古树AB的高.小王拿尺子量得古树在地面上的影子BC=8米,在斜坡上面的影子CD=6米,测得斜坡CD与地面成∠DCE=30°,同一时刻小李量的1.5米的旗杆在地上面的影子长是2米.请你根据以上数据算出古树的高.
分析 作DH⊥CE于H,延长AD交CE于F,如图,在Rt△CDH中利用含30度的直角三角形三边的关系得到DH=$\frac{1}{2}$CD=3,CH=$\sqrt{3}$DH=3$\sqrt{3}$,由于同一时刻小李量的1.5米的旗杆在地上面的影子长是2米,根据相似的性质得$\frac{DH}{HF}$=$\frac{1.5}{2}$,可计算出HF=4,然后利用$\frac{AB}{BF}$=$\frac{1.5}{2}$即可计算出AB.
解答 解: 作DH⊥CE于H,延长AD交CE于F,如图,
作DH⊥CE于H,延长AD交CE于F,如图,
在Rt△CDH中,∵∠DCH=30°,
∴DH=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3,
CH=$\sqrt{3}$DH=3$\sqrt{3}$,
∵同一时刻小李量的1.5米的旗杆在地上面的影子长是2米,
∴$\frac{DH}{HF}$=$\frac{1.5}{2}$,
∴HF=4,
∴$\frac{AB}{BF}$=$\frac{1.5}{2}$,即$\frac{AB}{8+3\sqrt{3}+4}$=$\frac{1.5}{2}$,
∴AB=$\frac{36+9\sqrt{3}}{4}$(m),
即古树的高为$\frac{36+9\sqrt{3}}{4}$m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度;借助标杆或直尺测量物体的高度.

练习册系列答案
相关题目
 如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:
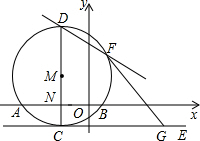 如图,⊙M与x轴交于A、B两点,其坐标分别为A(-3,0)、B(1,0),直径CD⊥x轴于N,抛物线y=-x2-2x+m经过A、B、D三点,
如图,⊙M与x轴交于A、B两点,其坐标分别为A(-3,0)、B(1,0),直径CD⊥x轴于N,抛物线y=-x2-2x+m经过A、B、D三点,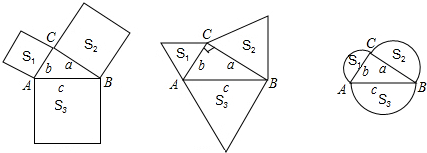
 如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数.
如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数.