题目内容
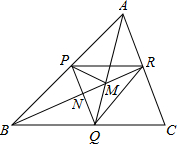如图，P，Q，R分别是△ABC三边上的点，四边形PQCR为平行四边形，BR，AQ交于M，PQ，BR交于N，若S△AMP=25，S△PBN=16，则S△CQR=考点：面积及等积变换
专题：计算题
分析：设BQ=a，CQ=b，S△AMP=S1，S△PBN=S2，S△ABC=S，根据平行四边形的性质得PM∥BQ，PQ∥AC，根据相似比和平行线分线段成比例定理得到
=
=
，
=
=
，易得PM=
，再根据三角形的面积公式得到
=
=
，同理可得
=
，然后计算
=
，根据平行四边形的性质得PR=CQ，CR=PQ，于是得到
=
，然后利用△BPQ∽△BAC得到
=
=
，所以
=
•
=
，于是易得S3=S1+S2=41．
| PA |
| AB |
| PM |
| BQ |
| PM |
| a |
| PA |
| AB |
| CQ |
| BC |
| b |
| a+b |
| ab |
| a+b |
| S1 |
| S |
| ||
|
| ab2 |
| (a+b)3 |
| S2 |
| S |
| a2b |
| (a+b)3 |
| S3 |
| S |
| ||
|
| S3 |
| S |
| PQ•b |
| (a+b)•CA |
| PQ |
| CA |
| BQ |
| BC |
| a |
| a+b |
| S3 |
| S |
| b |
| a+b |
| a |
| a+b |
| ab |
| (a+b)2 |
解答：
解：设BQ=a，CQ=b，S△AMP=S1，S△PBN=S2，S△ABC=S，
∵四边形PQCR为平行四边形，
∴PM∥BQ，PQ∥AC，
∴
=
=
，
=
=
，
∴
=
，即PM=
，
∴
=
，
∵PM∥BQ，
∴∠APM=∠ABC，
∴
=
•
•
=
，
同理可得
=
，
∵
=
，
∵四边形PQCR为平行四边形，
∴PR=CQ，CR=PQ，
∴
=
，
∵PQ∥AC，
∴△BPQ∽△BAC，
∴
=
=
，
∴
=
•
=
，
∴
+
=
=
+
=
=
=
，
∴S3=S1+S2=25+16=41．
故答案为41．
解：设BQ=a，CQ=b，S△AMP=S1，S△PBN=S2，S△ABC=S，∵四边形PQCR为平行四边形，
∴PM∥BQ，PQ∥AC，
∴
| PA |
| AB |
| PM |
| BQ |
| PM |
| a |
| PA |
| AB |
| CQ |
| BC |
| b |
| a+b |
∴
| PM |
| a |
| b |
| a+b |
| ab |
| a+b |
∴
| S1 |
| S |
| ||
|
∵PM∥BQ，
∴∠APM=∠ABC，
∴
| S1 |
| S |
| b |
| a+b |
| ab |
| a+b |
| 1 |
| a+b |
| ab2 |
| (a+b)3 |
同理可得
| S2 |
| S |
| a2b |
| (a+b)3 |
∵
| S3 |
| S |
| ||
|
∵四边形PQCR为平行四边形，
∴PR=CQ，CR=PQ，
∴
| S3 |
| S |
| PQ•b |
| (a+b)•CA |
∵PQ∥AC，
∴△BPQ∽△BAC，
∴
| PQ |
| CA |
| BQ |
| BC |
| a |
| a+b |
∴
| S3 |
| S |
| b |
| a+b |
| a |
| a+b |
| ab |
| (a+b)2 |
∴
| S1 |
| S |
| S2 |
| S |
| S1 |
| S |
| ab2 |
| (a+b)3 |
| a2b |
| (a+b)3 |
| ab(a+b) |
| (a+b)3 |
| ab |
| (a+b)2 |
| S3 |
| S |
∴S3=S1+S2=25+16=41．
故答案为41．
点评：本题考查了面积及等积变换：掌握三角形面积公式和平行线四边形的性质，熟练运用平行线分线段成比例定理和相似比进行线段的计算．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3）．
如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为
如图，已知△ABC与△BAD中，AC⊥AB，BD⊥AB，再选择下列条件中的一个条件，就可以用“HL”来说明△ABC≌△BAD，你选的条件是（ ）| A、∠ABC=∠BAD |
| B、∠ACB=∠BDA |
| C、AC=BD |
| D、BC=AD |
如图，Rt△AFC和Rt△AEB关于虚线成轴对称，现给出下列结论：