题目内容
如图1,若四边形ABCD、GFED都是正方形,显然图中有AG=CE,AG⊥CE.
(1)当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明,若不成立,请说明理由;
(2)当正方形GFED绕D旋转到B,D,G在一条直线(如图3)上时,连结CE,设CE分别交AG、AD于P、H.
①求证:AG⊥CE;
②如果,AD=2
,DG=
,求CE的长.

(1)当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明,若不成立,请说明理由;
(2)当正方形GFED绕D旋转到B,D,G在一条直线(如图3)上时,连结CE,设CE分别交AG、AD于P、H.
①求证:AG⊥CE;
②如果,AD=2
| 5 |
| 10 |

考点:四边形综合题
专题:
分析:(1)利用正方形性质以及全等三角形的判定的很粗△AGD≌△CED(SAS)即可得出答案;
(2)①根据(1)得出∠1=∠2,再利用∠3=∠4,∠4+∠2=90°,可得出∠3+∠1=90°,进而得出答案;
②利用等腰直角三角形的性质可得出MD=MG=
,进而利用勾股定理求出CE的长.
(2)①根据(1)得出∠1=∠2,再利用∠3=∠4,∠4+∠2=90°,可得出∠3+∠1=90°,进而得出答案;
②利用等腰直角三角形的性质可得出MD=MG=
| 5 |
解答:(1)解:AG=CE成立.
理由:∵四边形ABCD、四边形DEFG是正方形,
∴GD=DE,AD=DC,
∠GDE=∠ADC=90°,
∴∠GDA=90°-∠ADE=∠EDC,
在△AGD和△CED中,
∴△AGD≌△CED(SAS),
∴AG=CE;
(2)证明:①由(1)可知△AGD≌△CED,
∴∠1=∠2,
∵∠3=∠4,∠4+∠2=90°,
∴∠3+∠1=90°,
∴∠APH=90°,
∴AG⊥CH;
②解:过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°,
∴∠DGM=45°,
∵DG=
,
∴MD=MG=
,
在Rt△AMG中,由勾股定理,得
∴CE=AG=5
.
理由:∵四边形ABCD、四边形DEFG是正方形,
∴GD=DE,AD=DC,
∠GDE=∠ADC=90°,

∴∠GDA=90°-∠ADE=∠EDC,
在△AGD和△CED中,
|
∴△AGD≌△CED(SAS),
∴AG=CE;
(2)证明:①由(1)可知△AGD≌△CED,
∴∠1=∠2,
∵∠3=∠4,∠4+∠2=90°,
∴∠3+∠1=90°,
∴∠APH=90°,
∴AG⊥CH;
②解:过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°,
∴∠DGM=45°,
∵DG=
| 10 |
∴MD=MG=
| 5 |
在Rt△AMG中,由勾股定理,得
∴CE=AG=5
| 2 |
点评:此题主要考查了正方形的性质以及等腰直角三角形的性质和全等三角形的判定与性质等知识,熟练利用正方形性质得出相等线段和角是解题关键.

练习册系列答案
相关题目
如果36x2-Mxy+49y2是一个完全平方式,那么M的值有( )
| A、1764 | B、42 |
| C、±84 | D、84 |
在有理数-3,0,
,2.5中,属于非负数的数的个数为( )
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
 如图,△ABC中,DE是AB的垂直平分线,交BC于E,垂足为D.若△AEC的周长为8cm,AD=2cm,则△ABC的周长是
如图,△ABC中,DE是AB的垂直平分线,交BC于E,垂足为D.若△AEC的周长为8cm,AD=2cm,则△ABC的周长是 如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点
如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点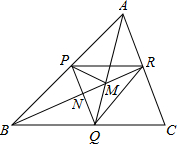 如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=
如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=