题目内容
 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求出以A、C、B、B1、C1、A1为顶点的六边形的面积.
考点:作图-轴对称变换
专题:
分析:(1)根据关于y轴对称的点的坐标特点画出△A1B1C1即可;
(2)根据各点在坐标系中的位置写出点A1,B1,C1的坐标;
(3)根据S六边形=S△ABC+S△A1B1C1+S矩形ABB1A1即可得出结论.
(2)根据各点在坐标系中的位置写出点A1,B1,C1的坐标;
(3)根据S六边形=S△ABC+S△A1B1C1+S矩形ABB1A1即可得出结论.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)由图可知,A1(1,5),B1(1,0),C1(4,3);
(3)S六边形=S△ABC+S△A1B1C1+S矩形ABB1A1
=
×5×3+
×5×3+2×5
=
+
+10
=25.
 解:(1)如图所示;
解:(1)如图所示;(2)由图可知,A1(1,5),B1(1,0),C1(4,3);
(3)S六边形=S△ABC+S△A1B1C1+S矩形ABB1A1
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 15 |
| 2 |
| 15 |
| 2 |
=25.
点评:本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
 如图,△ABC中,DE是AB的垂直平分线,交BC于E,垂足为D.若△AEC的周长为8cm,AD=2cm,则△ABC的周长是
如图,△ABC中,DE是AB的垂直平分线,交BC于E,垂足为D.若△AEC的周长为8cm,AD=2cm,则△ABC的周长是 如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点
如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点 如图,在平面直角坐标系中,每个小正方形的边长均为1个单位,△ABC的顶点均在格点上.
如图,在平面直角坐标系中,每个小正方形的边长均为1个单位,△ABC的顶点均在格点上. 如图,P为△ABC的BC边上的点,PD∥AC,交AB于点D,PE∥AB,交AC于点E.已知△ABC的面积为5cm2,BC=2cm,设BP的长为x cm
如图,P为△ABC的BC边上的点,PD∥AC,交AB于点D,PE∥AB,交AC于点E.已知△ABC的面积为5cm2,BC=2cm,设BP的长为x cm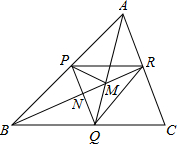 如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=
如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=