题目内容
 如图,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:
如图,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:①∠1=∠2;②△ANC≌△AMB;③CD=DN,
其中正确的结论是
考点:轴对称的性质,全等三角形的判定与性质
专题:
分析:首先利用轴对称的性质分别判断正误,然后选择一个进行证明即可.
解答:解:①∵Rt△AFC和Rt△AEB关于虚线成轴对称,
∴∠MAD=∠NAD,∠EAD=∠FAD,
∴∠EAD-∠MAD=∠FAD-∠NAD,
即:∠1=∠2,故正确;
②∵Rt△AFC和Rt△AEB关于虚线成轴对称,
∴∠B=∠C,AC=AB,
在△ANC与△AMB中,
∴△ANC≌△AMB,故正确;
③易得:CD=BD,
但在三角形DNB中,DN不一定等于BD,
故错误.
故答案为:①②.
∴∠MAD=∠NAD,∠EAD=∠FAD,
∴∠EAD-∠MAD=∠FAD-∠NAD,
即:∠1=∠2,故正确;
②∵Rt△AFC和Rt△AEB关于虚线成轴对称,
∴∠B=∠C,AC=AB,
在△ANC与△AMB中,
|
∴△ANC≌△AMB,故正确;
③易得:CD=BD,
但在三角形DNB中,DN不一定等于BD,
故错误.
故答案为:①②.
点评:本题考查轴对称的性质,熟练掌握性质是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 已知:⊙O是数轴的以原点为圆心1为半径的圆,∠AOB=45°.点P是数轴上一个动点,若过P点且与OA平行(包括重合)的直线与⊙O有公共点,设P在数轴上对应的数为x,则x的取值范围是( )
已知:⊙O是数轴的以原点为圆心1为半径的圆,∠AOB=45°.点P是数轴上一个动点,若过P点且与OA平行(包括重合)的直线与⊙O有公共点,设P在数轴上对应的数为x,则x的取值范围是( )| A、-1≤x≤1 | ||||
B、-
| ||||
C、0≤x≤
| ||||
D、x>
|
 如图,二次函数y=ax2+bx+c图象的一部分,其中对称轴为x=-1,且过(-3,0),下列说法:
如图,二次函数y=ax2+bx+c图象的一部分,其中对称轴为x=-1,且过(-3,0),下列说法:①abc<0;
②2a<b;
③4a+2b+c=0;
④若(-5,y1),(5,y2)是抛物线上的点,则y1<y2.
其中说法正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
△ABC中,∠B=∠C,与△ABC全等的另一个三角形中有一个角为91°,那么91°角在△ABC中的对应角是
( )
( )
| A、∠A | B、∠B |
| C、∠C | D、∠B或∠C |
 如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点
如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点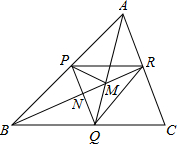 如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=
如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR= 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是