题目内容
已知函数y=ax2+x+1的图象与x轴只有一个公共点,则a的值为 .
考点:抛物线与x轴的交点
专题:计算题
分析:由抛物线与x轴只有一个公共点,得到根的判别式等于0,即可求出a的值.
解答:解:若a=0,函数解析式变形为y=x+1,与x轴只有一个公共点,符合题意;
若a≠0,由抛物线与x轴只有一个公共点,得到b2-4ac=1-4a=0,
解得:a=
,
综上,a的值为0或
.
故答案为:0或
若a≠0,由抛物线与x轴只有一个公共点,得到b2-4ac=1-4a=0,
解得:a=
| 1 |
| 4 |
综上,a的值为0或
| 1 |
| 4 |
故答案为:0或
| 1 |
| 4 |
点评:此题考查了抛物线与x轴的交点,注意分a=0与a≠0两种情况考虑.

练习册系列答案
相关题目
△ABC中,∠B=∠C,与△ABC全等的另一个三角形中有一个角为91°,那么91°角在△ABC中的对应角是
( )
( )
| A、∠A | B、∠B |
| C、∠C | D、∠B或∠C |
已知样本数据1,3,4,2,5,下列说法不正确的是( )
| A、平均数是3 | B、中位数是4 |
| C、极差是4 | D、方差是2 |
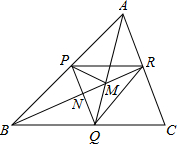 如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR=
如图,P,Q,R分别是△ABC三边上的点,四边形PQCR为平行四边形,BR,AQ交于M,PQ,BR交于N,若S△AMP=25,S△PBN=16,则S△CQR= 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是