题目内容
5.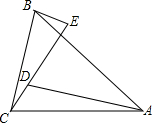 如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.
如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.(1)求证:△ACD≌△CBE;
(2)如果AD=25cm,DE=17cm,求BE的长.
分析 (1)易证∠CDA=∠BEC,即可证明△ACD≌△BCE;
(2)根据(1)中结论可得AD=CE,CD=BE,进而解答即可.
解答 证明:(1)∵∠E=100°,
∴∠BCE+∠CBE=80°,
∵∠CAD=∠BCE,∠ACB=80°,
∴∠CDA=∠BEC,
在△ACD与△CBE中,
$\left\{\begin{array}{l}{∠CDA=∠BEC}\\{AC=BC}\\{∠CAD=∠BCE}\end{array}\right.$,
∴△ACD≌△CBE(ASA),
(2)∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∴BE=25-17=8cm.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
相关题目
15. 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )| A. | 2a-b | B. | b-2a | C. | -b | D. | b |
10.观察下列单项式的排列规律:3x,-7x2,11x3,-15x4,19x5,…,照这样排列第10个单项式应是( )
| A. | 39x10 | B. | -39x10 | C. | -43x10 | D. | 43x10 |