Question

2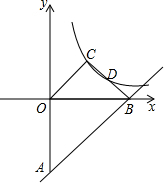．如图，直线y=x-4与y轴、x轴分别交于点A、B，点C为双曲线y=$\frac{k}{x}$上一点，OC∥AB，连接BC交双曲线于点D，点D恰好是BC的中点，则k的值是（　　）

• A． $\frac{16}{9}$
• B． 2
• C． 4
• D． $\frac{4}{3}$

Answer 1

分析 先确定出B坐标，根据OC∥AB，利用两直线平行时斜率相等确定出直线OC的解析式，与反比例函数解析式联立表示出C坐标，再利用线段中点坐标公式表示出D坐标，代入反比例解析式中列出关于k的方程，求出方程的解即可得到k的值．

解答 解：对于直线y=x-4，
令y=0，得到x=4，
∴B（4，0），
∵OC∥AB，
∴直线OC解析式为y=x，
y=x与反比例解析式联立消去y得：$\frac{k}{x}$=x，
去分母得：x²=k，
解得：x=$\sqrt{k}$或x=-$\sqrt{k}$（舍去），
∴y=$\sqrt{k}$．
∴C（$\sqrt{k}$，$\sqrt{k}$），
∵D为BC中点，
∴D（$\frac{4+\sqrt{k}}{2}$，$\frac{\sqrt{k}}{2}$），
将D坐标代入反比例解析式得：$\frac{4+\sqrt{k}}{2}$•$\frac{\sqrt{k}}{2}$=k，
解得：k=$\frac{16}{9}$．
故选A．

点评 此题考查了一次函数与反比例函数的交点问题，涉及的知识有：线段中点坐标公式，两直线平行时斜率满足的关系，一次函数与坐标轴的交点，以及坐标与图形性质，是一道中档题．