题目内容
7.在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=$\frac{6}{x}$的一个交点为N(3,n),与x轴、y轴分别交于点A、B.(1)求n的值;
(2)若NA=2AB,求k的值.
分析 (1)将点N的坐标代入反比例函数的解析式即可求得m的值;
(2)作NC⊥x轴于点C,把N点的坐标代入y=kx+b,求得b=2-3k,根据NA=2AB得到AB=BN,AO=CO,根据三角形中位线定理得出OB=$\frac{1}{2}$NC,即2-3k=1,解得即可.
解答  解:(1)∵双曲线y=$\frac{6}{x}$经过N(3,n),
解:(1)∵双曲线y=$\frac{6}{x}$经过N(3,n),
∴3n=6,
解得:n=2;
(2)点N(3,2)在y=kx+b上,
∴2=3k+b,
∴b=2-3k,
∵NA=2AB,
∴AB=NB,则OA=OC,
∴OB=$\frac{1}{2}$NC,即2-3k=1,
解得k=$\frac{1}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是表示出OB的出,然后利用线段之间的倍数关系确定k的值,难度不大.

练习册系列答案
相关题目
2.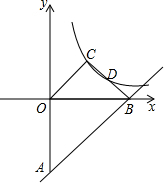 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )| A. | $\frac{16}{9}$ | B. | 2 | C. | 4 | D. | $\frac{4}{3}$ |
 一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.
一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程. 若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.
若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$. 如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An-1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An-1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数$y=\frac{16}{x}(x>0)$的图象上,则y1+y2+y3+…+yn=4$\sqrt{n}$.
如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An-1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An-1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数$y=\frac{16}{x}(x>0)$的图象上,则y1+y2+y3+…+yn=4$\sqrt{n}$.