题目内容
13. 如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是( )
如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是( )| A. | 3 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 由矩形的性质和已知条件∠EDC:∠EDA=1:3,可得△CDE∽△ADE,再由AC=8,即可求得DE的长度.
解答 解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=8,OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=4,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°-∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴2DE2=OD2=16,
∴DE=2$\sqrt{2}$.
点评 此题主要考查了相似三角形的判定和矩形的性质,根据已知得出OE2+DE2=OD2是解题关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
3.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列一组数:1,4,0,$-\frac{1}{2}$,-3在数轴上表示的点中,不在原点右边的点的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.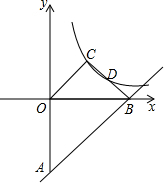 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )| A. | $\frac{16}{9}$ | B. | 2 | C. | 4 | D. | $\frac{4}{3}$ |
 如图,已知:∠1=∠2,∠A=∠DCE,说明∠E=∠F的理由.
如图,已知:∠1=∠2,∠A=∠DCE,说明∠E=∠F的理由. 一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.
一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.