题目内容
17. 如图,在Rt△ABC中,∠B=90°,点P以3cm/秒的速度从点B向点C移动.点Q以4cm/秒的速度从点B向点C移动,问经过几秒时△BPQ的面积为48cm2,此时PQ的距离是多少?
如图,在Rt△ABC中,∠B=90°,点P以3cm/秒的速度从点B向点C移动.点Q以4cm/秒的速度从点B向点C移动,问经过几秒时△BPQ的面积为48cm2,此时PQ的距离是多少?
分析 设P、Q运行时间为x秒,△BPQ的面积为ycm2,由题意可找出y关于x的关系式,代入y=48cm2,即可求得运行时间,根据时间可得知BP、BQ的长度,结合勾股定理既能得出结论.
解答 解:设P、Q运行时间为x秒,△BPQ的面积为ycm2,
则有y=3x×4x÷2=6x2(x≥0),
当y=48cm2时,6x2=48,
解得:x=2$\sqrt{2}$,
当x=2$\sqrt{2}$秒时,BP=6$\sqrt{2}$cm,BQ=8$\sqrt{2}$cm,
由勾股定理得:PQ=$\sqrt{B{P}^{2}+B{Q}^{2}}$=10$\sqrt{2}$cm.
点评 本题考查了一元二次方程的应用,解题的关键是利用已知条件找出正确的一元二次方程,再利用开方法求出方程解.

练习册系列答案
相关题目
8.下列一组数:1,4,0,$-\frac{1}{2}$,-3在数轴上表示的点中,不在原点右边的点的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.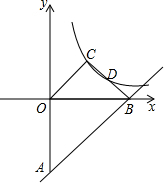 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )| A. | $\frac{16}{9}$ | B. | 2 | C. | 4 | D. | $\frac{4}{3}$ |
