题目内容
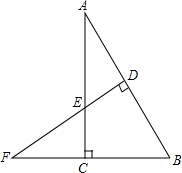 如图,在Rt△ABC中,∠ACB=90°,AB=6,∠A=30°,AB的垂直平分线DE角BC的延长线于F,则FB的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB=6,∠A=30°,AB的垂直平分线DE角BC的延长线于F,则FB的长是( )| A、6 | B、8 | C、5 | D、7 |
考点:线段垂直平分线的性质
专题:
分析:连接AF,根据直角三角形两锐角互余求出∠B=60°,再根据线段垂直平分线上的点到两端点的距离相等可得AF=BF,从而判断出△ABF是等边三角形,根据等边三角形的三条边都相等可得FB=AB.
解答: 解:如图,连接AF,
解:如图,连接AF,
∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
∵AB的垂直平分线DE交BC的延长线于F,
∴AF=BF,
∴△ABF是等边三角形,
∴FB=AB=6.
故选A.
 解:如图,连接AF,
解:如图,连接AF,∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
∵AB的垂直平分线DE交BC的延长线于F,
∴AF=BF,
∴△ABF是等边三角形,
∴FB=AB=6.
故选A.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
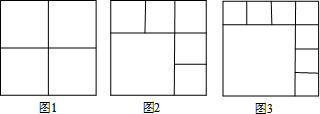
将一个正方形剪成n个小正方形,第一次操作按照图1所示,分割出4个正方形,第二次操作按如图2所示,分割出6个正方形,第三次操作按如图3所示,按照上述规律,则第n次操作,正方形的个数为( )

| A、(n+1)2 |
| B、3n+1 |
| C、2n |
| D、2n+2 |
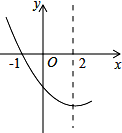 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )| A、①②③ | B、②④⑤ |
| C、①③⑤ | D、③④ |
函数:①y=
;②y=
;③y=2x+3;④y=-x2;⑤y=
-x,其中y是x的一次函数的个数为( )
| x |
| 3 |
| 1 |
| x |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
设p=
-
,q=
-
,则p,q的关系是( )
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
| A、p=q | B、p>q |
| C、p<q | D、p=-q |
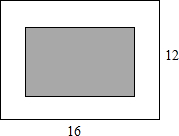 如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.
如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽. 如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于
如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于