题目内容
14.若凸边形的n个内角与某一个外角之和是1125°,求n.分析 根据n边形的内角和定理可知:n边形内角和为(n-2)×180.设这个外角度数为x度,利用方程即可求出答案.
解答 解:设这个外角度数为x°,根据题意,得
(n-2)×180+x=1125,
180n-360+x=1125,
x=1125+360-180n,即x=1485-180n,
由于0<x<180,即0<1485-180n<180,
可变为:$\left\{\begin{array}{l}{1485-180n>0}\\{1485-180n<180}\end{array}\right.$,
解得8$\frac{1}{4}$<n<9$\frac{1}{4}$,
所以n=9.
点评 本题主要考查了多边形的内角和定理:n边形的内角和为:180°•(n-2).同时考查了方程的变形及不等式组的解法.

练习册系列答案
相关题目
2.用科学记数法表示430 000是( )
| A. | 43×104 | B. | 4.3×105 | C. | 4.3×104 | D. | 4.3×106 |
9. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为(
如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为(
 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为(
如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为(| A. | 48° | B. | 54° | C. | 74° | D. | 78° |
6.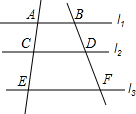 如图,已知l1∥l2∥l3,下列比例式中错误的是( )
如图,已知l1∥l2∥l3,下列比例式中错误的是( )
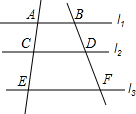 如图,已知l1∥l2∥l3,下列比例式中错误的是( )
如图,已知l1∥l2∥l3,下列比例式中错误的是( )| A. | $\frac{AC}{CE}$=$\frac{BD}{DF}$ | B. | $\frac{AC}{AE}$=$\frac{BD}{BF}$ | C. | $\frac{CE}{AE}$=$\frac{DF}{BF}$ | D. | $\frac{AE}{BF}$=$\frac{BD}{AC}$ |
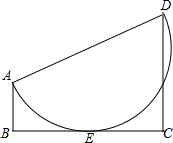 已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.
已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.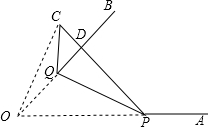 如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.
如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.