题目内容
4.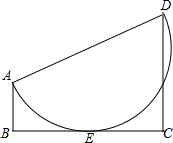 已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.
已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.
分析 连结AE、ED,由平行线的性质推出∠B=∠C,由AD为直径,得出∠AED=90°,从而证得∠AEB=∠CDE=90°-∠DEC,根据相似三角形的判定证得△ABE∽△ECD,由相似三角形的性质即可证得结论.
解答 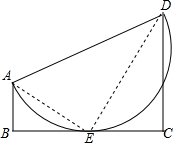 解:连结AE、ED,
解:连结AE、ED,
∵AB∥CD,∠B=90°,
∴∠C=90°,
∴∠B=∠C,
∵AD为直径,
∴∠AED=90°,
∠AEB=∠CDE=90°-∠DEC,
∴△ABE∽△ECD,
∴$\frac{AB}{EC}=\frac{BE}{CD}$,
∴AB•CD=BE•EC.
点评 本题主要考查了直径所对的圆周角的性质,相似三角形的判定和性质,能证得∠AEB=∠CDE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列各对数中,互为相反数的是( )
| A. | -|-7|和+(-7) | B. | +(-10)和-(+10) | ||
| C. | 0和绝对值最小的数 | D. | -1和2-3 |
12. 有理数a、b在数轴上的对应的位置如图所示:则( )
有理数a、b在数轴上的对应的位置如图所示:则( )
 有理数a、b在数轴上的对应的位置如图所示:则( )
有理数a、b在数轴上的对应的位置如图所示:则( )| A. | -a<-b | B. | -b<a | C. | b=a | D. | -a>b |
9.(-10)×(-0.3×102)×(-0.4×105)等于( )
| A. | 1.2×108 | B. | -1.2×108 | C. | 1.2×107 | D. | -1.2×107 |
16. 如图,在等边△ABC中,点D、E分别为AB、AC的中点,则∠ADE的度数是( )
如图,在等边△ABC中,点D、E分别为AB、AC的中点,则∠ADE的度数是( )
 如图,在等边△ABC中,点D、E分别为AB、AC的中点,则∠ADE的度数是( )
如图,在等边△ABC中,点D、E分别为AB、AC的中点,则∠ADE的度数是( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |