题目内容
3.AD是△ABC的中线,设△ABD的面积为S1,△ACD的面积为S2,那么( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | S1≠S2 |
分析 根据三角形的中线的性质进行解答即可.
解答 解:∵AD是△ABC的中线,△ABD的面积为S1,△ACD的面积为S2,
∴△ABD的面积为S1=△ACD的面积为S2,
故选B.
点评 此题考查三角形的面积问题,关键是根据三角形的中线把三角形分成两个面积相等的部分进行解答.

练习册系列答案
相关题目
11.四舍五入得到的近似数0.098,下列说法正确的是( )
| A. | 精确到万位 | B. | 精确到百分位 | C. | 精确到千分位 | D. | 精确到十分位 |
12.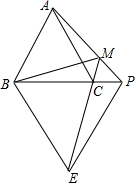 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
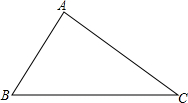 如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法?
如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法? △ABC中,AB=AC,∠CAB=120°,DE垂直平分AB,则∠ADC=60°.
△ABC中,AB=AC,∠CAB=120°,DE垂直平分AB,则∠ADC=60°.