题目内容
12.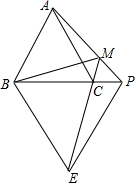 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
分析 根据等腰三角形的性质得到AB=BC,∠ABP=∠CBE=60°,PB=PE,证得△APB≌△CEB (SAS),根据全等三角形的性质得到∠APB=∠CEB,于是得到∠PME=∠PBE=60゜,作BN⊥AM于N,BF⊥ME于F,通过△BNP≌△BFE(AAS),得到BN=BF,根据角平分线的性质得到BM平分∠AME,求得∠AMB=$\frac{1}{2}∠$AME=$\frac{1}{2}×120°$=60°,根据三角形的内角和即可得到结论.
解答 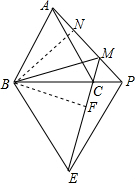 证明:∵等边△ABC和等边△BPE,
证明:∵等边△ABC和等边△BPE,
∴AB=BC,∠ABP=∠CBE=60°,PB=PE,
在△APB和△CEB中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBE}\\{BP=BE}\end{array}\right.$,
∴△APB≌△CEB (SAS),
∴∠APB=∠CEB,
∵∠MCP=∠BCE,
∴∠PME=∠PBE=60゜,
作BN⊥AM于N,BF⊥ME于F,
∵△APB≌△CEB,
∴BP=BE,∠BPN=∠FEB,
在△BNP和△BFE中,
$\left\{\begin{array}{l}{∠BNP=∠BFE}\\{∠NPB=∠FEB}\\{PB=EB}\end{array}\right.$,
∴△BNP≌△BFE(AAS),
∴BN=BF,
∴BM平分∠AME,
∴∠AMB=$\frac{1}{2}∠$AME=$\frac{1}{2}×120°$=60°,
∵∠ABM=40°,
∴∠BAP=80°,
∴∠APB=180°-∠ABP-∠BAP=40°.
故选A.
点评 此题主要考查了全等三角形的判定与性质,等边三角形的性质,角平分线的性质,三角形的内角和,熟练掌握全等三角形的判定是解题关键.

| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | S1≠S2 |
| A. | (2,1) | B. | (-2,1) | C. | (2,-1) | D. | (-2,-1) |
| A. | -2 | B. | 2 | C. | -8 | D. | 8 |