题目内容
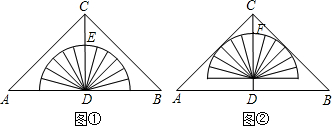
如图①,将量角器与等腰直角△ABC纸片放置成轴对称图形,已知∠ACB=90°,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,测得CE=5cm,将量角器沿DC方向平移2cm,半圆(量角器)恰与△ABC的边AC、BC相切,如图②,则AB的长为( )

A、8+3
| ||
B、8+6
| ||
C、4+6
| ||
D、16+6
|
考点:相似三角形的判定与性质,勾股定理,等腰直角三角形,切线的性质
专题:
分析:如图,设图②中半圆的圆心为O,与BC的切点为M,连接OM,根据切线的性质可以得到∠OMC=90°,而根据已知条件可以得到∠DCB=45°,设AB为2x,根据等腰直角三角形的性质得到CD=BD=x,而CE=5cm,又将量角器沿DC方向平移2cm,由此得到半圆的半径为x-5,OC=x-2,然后在Rt△OCM中利用三角函数可以列出关于x的方程,解方程即可求解.
解答: 解:如图,设图②中半圆的圆心为O,与BC的切点为M,
解:如图,设图②中半圆的圆心为O,与BC的切点为M,
连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知道∠DCB=45°,
设AB为2x,
∵△ABC是等腰直角三角形,
∴CD=BD=x,
而CE=5cm,又将量角器沿DC方向平移2cm,
∴半圆的半径为x-5,OC=x-2,
∴sin∠DCB=
=
,
∴
=
,
∴x=
,
∴AB=2x=2×
=16+6
(cm).
故选:D.
 解:如图,设图②中半圆的圆心为O,与BC的切点为M,
解:如图,设图②中半圆的圆心为O,与BC的切点为M,连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知道∠DCB=45°,
设AB为2x,
∵△ABC是等腰直角三角形,
∴CD=BD=x,
而CE=5cm,又将量角器沿DC方向平移2cm,
∴半圆的半径为x-5,OC=x-2,
∴sin∠DCB=
| OM |
| CO |
| ||
| 2 |
∴
| x-5 |
| x-2 |
| ||
| 2 |
∴x=
10-2
| ||
2-
|
∴AB=2x=2×
10-2
| ||
2-
|
| 2 |
故选:D.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在矩形ABCD中,DE⊥AC于点E,设∠ADE=a,且cosa=
如图所示,在矩形ABCD中,DE⊥AC于点E,设∠ADE=a,且cosa=| 3 |
| 5 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于
如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于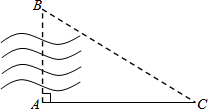 如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈
如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈ ⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长.
⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长.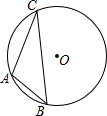 如图,⊙O为△ABC的外接圆,
如图,⊙O为△ABC的外接圆,
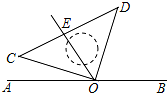 如图,一直角三角板COD的直角(∠COD=90°)顶点O落在直线AB上,射线OE平分∠AOD.
如图,一直角三角板COD的直角(∠COD=90°)顶点O落在直线AB上,射线OE平分∠AOD. 如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数
如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数