题目内容
5.x取何值时,下列各式在实数范围内有意义:(1)$\sqrt{x-3}$+$\sqrt{5-x}$;
(2)$\sqrt{{-(x-2)}^{2}}$;
(3)$\sqrt{x-3}$+$\sqrt{3-x}$
(4)$\frac{\sqrt{x+1}}{\sqrt{x}-2}$.
分析 (1)根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-3≥0}\\{5-x≥0}\end{array}\right.$,再解不等式组即可;
(2)根据二次根式有意义的条件可得x-2=0,解方程即可;
(3)根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-3≥0}\\{3-x≥0}\end{array}\right.$,再解不等式组即可;
(4)根据二次根式和分式有意义的条件可得x+1≥0,x≥0且x≠4,再解不等式组即可.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{x-3≥0}\\{5-x≥0}\end{array}\right.$,
解得:3≤x≤5;
(2)∵(x-2)2≥0,
∴-(x-2)2≤0,
根据二次根式有意义的条件可得x-2=0,
解得:x=2;
(3)由题意得:$\left\{\begin{array}{l}{x-3≥0}\\{3-x≥0}\end{array}\right.$,
解得:x=3;
(4)由题意得:x+1≥0,x≥0且x≠4,
解得:x≥0且x≠4.
点评 此题主要考查了二次根式和分式有意义的条件,分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
相关题目
20.如图所示的四个函数图象中,y随x的增大而增大的是( )
| A. | 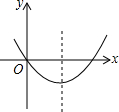 | B. | 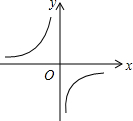 | C. | 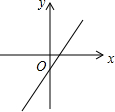 | D. | 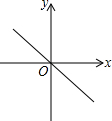 |
15.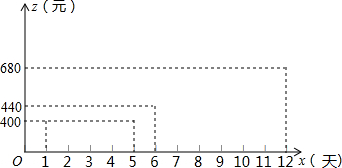 在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:
在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:
由于机器损耗等原因,当每天生产的服装数达到一定量后,平均每套服装的成本会随着服装产量的增加而增大,这样平均每套服装的成本z(元)与生产时间x(天)的关系如图所示.
(1)判断每天生产的服装的数量y(套)与生产时间x(元)之间是我们学过的哪种函数关系?并验证.
(2)已知这批外贸服装的订购价格为每套1570元,设车间每天的利润为w(元).求w(元)与x(天)之间的函数关系式,并求出哪一天该生产车间获得最高利润,最高利润是多少元?
(3)从第6天起,该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金,但必须保证每天扣除捐款后的利润随时间的增大而增大.求a的最大值,此时留守儿童共得多少元基金?
 在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:
在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:| 时间x(天) | 1 | 2 | 3 | 4 | … |
| 每天产量y(套) | 22 | 24 | 26 | 28 | … |
(1)判断每天生产的服装的数量y(套)与生产时间x(元)之间是我们学过的哪种函数关系?并验证.
(2)已知这批外贸服装的订购价格为每套1570元,设车间每天的利润为w(元).求w(元)与x(天)之间的函数关系式,并求出哪一天该生产车间获得最高利润,最高利润是多少元?
(3)从第6天起,该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金,但必须保证每天扣除捐款后的利润随时间的增大而增大.求a的最大值,此时留守儿童共得多少元基金?
 如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.
如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.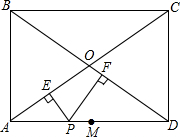 矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.
矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF. 已知直角三角形面积是8平方厘米,求阴影部分面积.
已知直角三角形面积是8平方厘米,求阴影部分面积.