题目内容
16.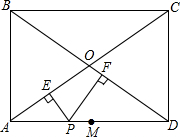 矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.
矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.
分析 连接OM、EF,证得O、F、E、P四点共圆和O、E、P、M四点共圆,从而得到O、F、E、M四点共圆,利用圆内接四边形的性质得到∠MEF=∠MFE,从而证得ME=MF.
解答 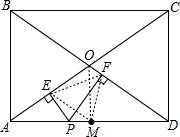 证明:连接OM、EF,
证明:连接OM、EF,
∵∠OEP=∠OFP=90°,
∴O、F、E、P四点共圆,
∵∠OEP+∠OMP=180°,
∴O、E、P、M四点共圆,
∴O、F、E、M四点共圆,
∴∠MFE=∠MOE,∠MEF=∠MOD,
∵OA=OB,AM=MD,
∴∠MOA=∠MOD,
∴∠MOE=∠MOD,
∴∠MEF=∠MFE,
∴ME=MF.
点评 本题考查了四点共圆的知识,解题的关键是能够利用证明四点共圆的判定方法进行判断,另外还应了解圆内接四边形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若化简|2-x|-$\sqrt{{x}^{2}-8x+16}$的结果是-2,则x的取值范围是( )
| A. | x为任意实数 | B. | 2≤x≤4 | C. | x≥4 | D. | x≤2 |
6.有5条线段长度分别为1,3,4,5,7,从中任取三条为一组,它们一定能构成三角形的频率为( )
| A. | 0.15 | B. | 0.10 | C. | 0.20 | D. | 0.30 |
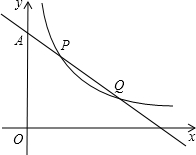 如图,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象与直线y2=k2x+b交于P(3,7)、Q两点.
如图,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象与直线y2=k2x+b交于P(3,7)、Q两点.