题目内容
(1)
(代入法);
(2)
(加减法);
(3)
;
(4)
.
|
(2)
|
(3)
|
(4)
|
考点:解二元一次方程组
专题:计算题
分析:(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答:解:(1)
,
由①得:x=y+4,
代入②得:2y+8+y=5,即y=-1,
把y=-1代入得:x=3,
则方程组的解为
;
(2)
,
①×5-②得:6x=3,即x=0.5,
把x=0.5代入①得:y=5,
则方程组的解为
;
(3)方程组整理得:
,
①-②得:4y=-16,即y=-4,
把y=-4代入①得:x=6,
则方程组的解为
;
(4)方程组整理得:
,
①×4-②得:x=200,
把x=200代入①得:y=300,
则方程组的解为
.
|
由①得:x=y+4,
代入②得:2y+8+y=5,即y=-1,
把y=-1代入得:x=3,
则方程组的解为
|
(2)
|
①×5-②得:6x=3,即x=0.5,
把x=0.5代入①得:y=5,
则方程组的解为
|
(3)方程组整理得:
|
①-②得:4y=-16,即y=-4,
把y=-4代入①得:x=6,
则方程组的解为
|
(4)方程组整理得:
|
①×4-②得:x=200,
把x=200代入①得:y=300,
则方程组的解为
|
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
设a、b是方程x2+x-2014=0的两个实数根,则a2+2a+b的值为( )
| A、2014 | B、2013 |
| C、2012 | D、2011 |
下列各式中,一定能成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

 如图,请画出△ABC关于点O点为对称中心的对称图形.
如图,请画出△ABC关于点O点为对称中心的对称图形.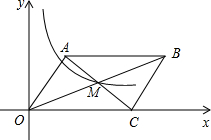 在直角坐标系中,?OCBA的边OC在x轴的正半轴上,点O为坐标原点,点B的坐标为(10,4),点M为对角线AC、OB的交点,反比例函数的图象经过点M,则该反比例函数的解析式为
在直角坐标系中,?OCBA的边OC在x轴的正半轴上,点O为坐标原点,点B的坐标为(10,4),点M为对角线AC、OB的交点,反比例函数的图象经过点M,则该反比例函数的解析式为