题目内容
解方程:
=
-
.
1+
|
| 2x+1 |
| x-1 |
考点:无理方程
专题:
分析:先将原方程变形为x+
+2
=2x+1,再设
=t(t≥0),则t2-2t-1=0,最后解这个意愿二次方程组就可以求出t的值,然后代入等式
=t就可以求出x的值.
| 1 |
| x |
x-
|
x-
|
x-
|
解答:解:由原方程移项,得
+
=
,
两边平方,得
x+
+2
=2x+1,
移项、合并同类项,得
(x-
)-2
-1=0;
设
=t(t≥0),则
t2-2t-1=0,
解得t=1±
,
∵t≥0,
∴t=1+
,
∴
=1+
,
∴x=
.
∵x≥1,
∴x=
,
经检验x=
原方程的根.
1+
|
| x-1 |
| 2x+1 |
两边平方,得
x+
| 1 |
| x |
x-
|
移项、合并同类项,得
(x-
| 1 |
| x |
x-
|
设
x-
|
t2-2t-1=0,
解得t=1±
| 2 |
∵t≥0,
∴t=1+
| 2 |
∴
x-
|
| 2 |
∴x=
3+2
| ||||||
| 2 |
∵x≥1,
∴x=
3+2
| ||||||
| 2 |
经检验x=
3+2
| ||||||
| 2 |
点评:本题是一道无理方程,考查了用换元法在解无理方程的运用,在解答的过程中注意检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
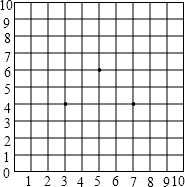 在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.
在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.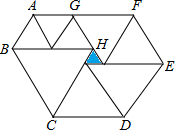 如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长?
如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长? 如图,⊙O1在⊙O2上无滑动地滚动4周后,刚好回到原来的位置,则⊙O1与⊙O2的面积之比为
如图,⊙O1在⊙O2上无滑动地滚动4周后,刚好回到原来的位置,则⊙O1与⊙O2的面积之比为 由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y-x的值为( )
由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y-x的值为( )