题目内容
17.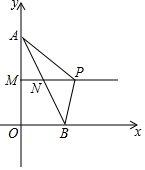 如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P,若△ABP是直角三角形,则点P的坐标是(2$\sqrt{5}$+2,4)或(12,4).
如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P,若△ABP是直角三角形,则点P的坐标是(2$\sqrt{5}$+2,4)或(12,4).
分析 根据勾股定理得到AB=4$\sqrt{5}$,根据三角形中位线的性质得到AM=OM=4,MN=2,AN=BN=2$\sqrt{5}$,①当∠APB=90°时,根据直角三角形的性质得到PN=AN=2$\sqrt{5}$,于是得到P(2$\sqrt{5}$+2,4),②当∠ABP=90°时,如图,过P作PC⊥x轴于C,根据相似三角形的性质得到BP=AB=4$\sqrt{5}$,根据勾股定理得到PN=2$\sqrt{30}$,求得P(2$\sqrt{30}$+2,4).
解答 解:∵点A(0,8),点B(4,0),
∴OA=8,OB=4,
∴AB=4$\sqrt{5}$,
∵点M,N分别是OA,AB的中点,
∴AM=OM=4,MN=2,AN=BN=2$\sqrt{5}$,
①当∠APB=90°时,
∵AN=BN,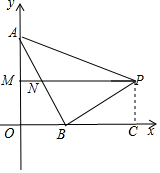
∴PN=AN=2$\sqrt{5}$,
∴PM=MN+PN=2$\sqrt{5}$+2,
∴P(2$\sqrt{5}$+2,4),
②当∠ABP=90°时,如图,
过P作PC⊥x轴于C,
则△ABO∽△BPC,
∴$\frac{AB}{PB}=\frac{OB}{PC}$=$\frac{4}{4}$=1,
∴BP=AB=4$\sqrt{5}$,
∴PC=OB=4,
∴BC=8,
∴PM=OC=4+8=12,
∴P(12,4),
故答案为:(2$\sqrt{5}$+2,4)或(12,4).
点评 本题考查了勾股定理,相似三角形的判定和性质,坐标与图形性质,直角三角形的性质,正确的理解题意是解题的关键.

练习册系列答案
相关题目
7.一个容量为80的样本中最大数是142,最小数是50,取组距为10,可以分成( )
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
5.已知$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{3x+3y=m-1}\\{nx-y=4}\end{array}\right.$的解,则nm的值为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
12.蜜蜂建造的蜂巢既坚固又省料,其厚度约为0.000073米,将0.000073用科学记数法表示为( )
| A. | 7.3×10-5 | B. | 7.3×10-4 | C. | 7.3×10-6 | D. | 73×10-6 |
2.算式(-2)×|-5|-|-3|之值为何( )
| A. | 13 | B. | 7 | C. | -13 | D. | -7 |
9.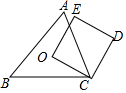 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )| A. | O是△AEB的外心,O是△AED的外心 | |
| B. | O是△AEB的外心,O不是△AED的外心 | |
| C. | O不是△AEB的外心,O是△AED的外心 | |
| D. | O不是△AEB的外心,O不是△AED的外心 |
6.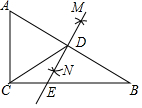 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )| A. | ∠ADE=∠ACB | B. | ∠A=∠ADC | C. | ∠B=∠DCB | D. | ∠A=∠BED |
 如图,直线y1=-2x+1与直线y2=x-5交于点A.
如图,直线y1=-2x+1与直线y2=x-5交于点A.