题目内容
6.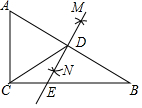 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB) 为半径作弧,两弧相交于M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )| A. | ∠ADE=∠ACB | B. | ∠A=∠ADC | C. | ∠B=∠DCB | D. | ∠A=∠BED |
分析 利用线段垂直平分线的性质,直角三角形斜边中线的性质、等腰三角形的性质一一判断即可.
解答  解:由题意,MN垂直平分AB,
解:由题意,MN垂直平分AB,
∴AD=BD,∠ADE=∠ACB=90°,故①正确,
∴CD=AD=DB,
∴∠B=∠DCB,故③正确,
∵∠B+∠DEB=90°,∠B+∠A=90°,
∴∠A=∠BED,故D正确,
无法证明∠A=∠ADC,
故选B.
点评 本题考查线段垂直平分线的性质,直角三角形斜边中线的性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
14. 在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
 在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )| A. | 20,20 | B. | 32.4,30 | C. | 32.4,20 | D. | 20,30 |

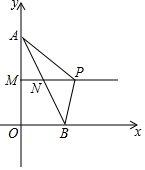 如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P,若△ABP是直角三角形,则点P的坐标是(2$\sqrt{5}$+2,4)或(12,4).
如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P,若△ABP是直角三角形,则点P的坐标是(2$\sqrt{5}$+2,4)或(12,4).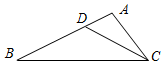 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )