题目内容
12.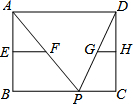 如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )
如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )| A. | 10 | B. | 5 | C. | 2.5 | D. | 无法确定 |
分析 E、F、G、H分别是AB、AP、DP、DC的中点,则EF,GH分别是△ABP,△DCP的中位线,得到EF+GH=$\frac{1}{2}$BC.
解答 解:在矩形ABCD中,BC=AD=10.
∵E、F、G、H分别为AB、AP、DP、DC的中点,
∴EF是△ABP的中位线,GH是△DPC的中位线,
∴EF+GH=$\frac{1}{2}$BP+$\frac{1}{2}$PC=$\frac{1}{2}$BC=5.
故选:B.
点评 本题主要考查了三角形的中位线定理.三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知反比例函数y=$\frac{k}{x}$的图象经过点(2,6),那么k的值为( )
| A. | 12 | B. | 3 | C. | -3 | D. | -12 |
7.2015年是“十二五”规划收官之年,济南市政府围绕“打造四个中心,建设现代泉城”中心任务,统筹推进稳增长,实现生产总值6200亿元,6200亿元用科学记数法表示为( )
| A. | 6.2×1010元 | B. | 6.2×1011元 | C. | 6.2×1012元 | D. | 0.62×1012元 |
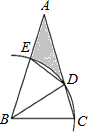 如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E
如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E