题目内容
13.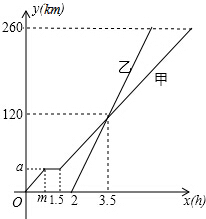 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶$\frac{1}{4}$或$\frac{11}{4}$小时后,两车恰好相距50km.
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶$\frac{1}{4}$或$\frac{11}{4}$小时后,两车恰好相距50km.
分析 根据“路程÷时间=速度”由函数图象就可以求出甲的速度,求出a的值和m的值,再求出甲、乙车行驶的路程y与时间x之间的解析式,由解析式之间的关系建立方程求出其解即可
解答 解:由题意,得
m=1.5-0.5=1.
120÷(3.5-0.5)=40,
则a=40.
当0≤x≤1时设y与x之间的函数关系式为y=k1x,由题意,得
40=k1,
则y=40x
当1<x≤1.5时,
y=40;
当1.5<x≤7设y与x之间的函数关系式为y=k2x+b,由题意,得$\left\{\begin{array}{l}{40=1.5{k}_{2}+b}\\{120=3.5{k}_{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=40}\\{b=-20}\end{array}\right.$,
则y=40x-20.
设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,由题意,得
$\left\{\begin{array}{l}{0=2{k}_{3}+{b}_{3}}\\{120=3.5{k}_{3}+{b}_{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{3}=80}\\{{b}_{3}=-160}\end{array}\right.$,
则y=80x-160.
当40x-20-50=80x-160时,
解得:x=$\frac{9}{4}$.
当40x-20+50=80x-160时,
解得:x=$\frac{19}{4}$.
$\frac{9}{4}$-2=$\frac{1}{4}$,$\frac{19}{4}-2$=$\frac{11}{4}$.
所以乙车行驶小时$\frac{1}{4}$或$\frac{11}{4}$小时,两车恰好相距50km,
故答案为$\frac{1}{4}$或$\frac{11}{4}$.
点评 本题考出了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出一次函数的解析式是关键.

 培优口算题卡系列答案
培优口算题卡系列答案| A. | 0.4×10-4 | B. | 4×10-5 | C. | 40×10-5 | D. | 4×105 |
| A. | 8cm | B. | 6cm | C. | 4cm | D. | 8cm或6cm |
| A. | 4>1 | B. | 3x-2<4 | C. | $\frac{1}{x}$<2 | D. | 4x-3<2y-7 |
| A. | $±\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $±\frac{{\sqrt{3}}}{4}$ |
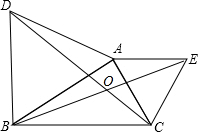 如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.
如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°. 如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.
如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.