题目内容
8.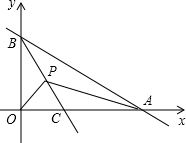 如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,由BC为∠ABO的平分线,可得PH=PD,则可得S1:S2=AB:OB,又因为OA、OB的长是方程x2-14x+48=0的两根(OA>OB),解方程即可求得OA,OB的长,则可得$\frac{{S}_{1}}{{S}_{2}}$的值.
解答  解:如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
解:如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
∵BC为∠ABO的平分线,
∴PH=PD,
∴S1:S2=AB:OB,
又∵OA、OB的长是方程x2-14x+48=0的两根(OA>OB),
解方程得:x1=8,x2=6,
∴OA=8,OB=6,
∴AB=10,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{AB}{OB}$=$\frac{5}{3}$.
点评 本题考查的是勾股定理,涉及到一元二次方程的应用、角平分线的性质等知识,难度适中.

练习册系列答案
相关题目
16. 如图,由B到A的方向是( )
如图,由B到A的方向是( )
 如图,由B到A的方向是( )
如图,由B到A的方向是( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
17.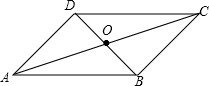 如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )
如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )
 如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )
如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )| A. | 32 | B. | 24 | C. | 21 | D. | 18 |
 如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.
如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.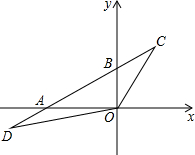 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).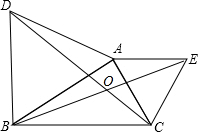 如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.
如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.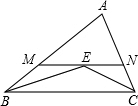 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )