题目内容
4.在△ABC中,∠C=90°,AC=1,BC=2,则sinA=$\frac{2\sqrt{5}}{5}$.分析 根据题意画出图形,由勾股定理求出AB的长,再根据三角函数的定义解答即可.
解答 解:如图:
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
sinA=$\frac{BC}{AB}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查锐角三角函数的定义,能熟记锐角三角函数定义是解此题的关键,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
19.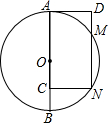 如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )
如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )
 如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )
如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
 在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线和平行线.
在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线和平行线.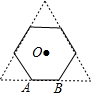 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.