题目内容
19.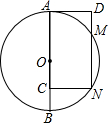 如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )
如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 连接ON,根据矩形的性质得到AC=DN=8,AD=CN,∠ACN=90°,根据已知条件得到BC=2,BO=ON=$\frac{1}{2}$AB=5,根据勾股定理得到CN=$\sqrt{O{N}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,即可得到结论.
解答  解:连接ON,
解:连接ON,
∵四边形ACND是矩形,
∴AC=DN=8,AD=CN,∠ACN=90°,
∵AB=10,
∴BC=2,BO=ON=$\frac{1}{2}$AB=5,
∴OC=3,
∴CN=$\sqrt{O{N}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AD=CN=4.
故选A.
点评 本题考查了垂径定理,勾股定理,矩形的性质,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
14.某校八年级(1)班50名学生参加2007年济宁市数学质量监测考试,全班学生的成绩统计如下表:
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数和中位数分别是多少?
(2)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中偏上水平?试说明理由.
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
(1)该班学生考试成绩的众数和中位数分别是多少?
(2)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中偏上水平?试说明理由.
9.抛物线y=-3(x+2)2-1的顶点坐标是( )
| A. | (2,-1) | B. | (2,1) | C. | (-2,-1) | D. | (-2,1) |
 如图半径是13cm圆柱形油槽,装入油后,油深CD为5cm,求油面宽度AB.
如图半径是13cm圆柱形油槽,装入油后,油深CD为5cm,求油面宽度AB.