题目内容
16. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.
分析 连接OC,可求得△OCD和扇形OCB的面积,进而可求出图中阴影部分的面积.
解答 解:连接OC, ∵过点C的切线交AB的延长线于点D,
∵过点C的切线交AB的延长线于点D,
∴OC⊥CD,
∴∠OCD=90°,
即∠D+∠COD=90°,
∵AO=CO,
∴∠A=∠ACO,
∴∠COD=2∠A,
∵∠A=∠D,
∴∠COD=2∠D,
∴3∠D=90°,
∴∠D=30°,
∴∠COD=60°
∵CD=3,
∴OC=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴阴影部分的面积=$\frac{1}{2}$×3×$\sqrt{3}$-$\frac{60π×3}{360}$=$\frac{3\sqrt{3}-π}{2}$,
故答案为:$\frac{3\sqrt{3}-π}{2}$.
点评 本题主要考查切线的性质及扇形面积的计算,掌握过切点的半径与切线垂直是解题的关键.求出∠D=30°是解题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列四个数中最大的数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
1. 已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
 已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )| A. | M | B. | N | C. | P | D. | Q |
8.在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
| A. | 甲、乙得分的平均数都是8 | |
| B. | 甲得分的众数是8,乙得分的众数是9 | |
| C. | 甲得分的中位数是9,乙得分的中位数是6 | |
| D. | 甲得分的方差比乙得分的方差小 |
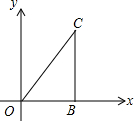 如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
 (1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.
(1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



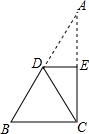
 将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.
将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.