题目内容
在△ABC中，∠C=90°，两直角边分别为a、b，且a、b满足方程a2-3ab+2b2=0，求sinA的值．
考点：解一元二次方程-因式分解法,勾股定理,锐角三角函数的定义
专题：计算题
分析：利用因式分解法求出方程的解，即可求出sinA的值．
解答：解：方程a2-3ab+2b2=0，
分解因式得：（a-2b）（a-b）=0，
可得a=2b或a=b，
当a=2b时，sinA=
=
；
当a=b时，sinA=
．
分解因式得：（a-2b）（a-b）=0，
可得a=2b或a=b，
当a=2b时，sinA=
| 2b | ||
|
2
| ||
| 5 |
当a=b时，sinA=
| ||
| 2 |
点评：此题考查了解一元二次方程-因式分解法，勾股定理，以及锐角三角函数定义，求出方程的解是解本题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
如图，一个无盖的正方体盒子的棱长为2，BC的中点为M，一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点，蚂蚁爬行的最短距离是（ ）A、
| ||
B、
| ||
| C、1 | ||
D、2+
|
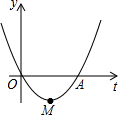如图，抛物线y=x2+bx+c过原点，且与x轴交于A（4，0），M为抛物线的顶点，问抛物线是否存在点P，使得∠POM=90°？若存在，求出点P坐标；若不存在，说明理由．