题目内容
7.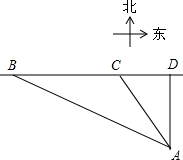 为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)
为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)
分析 先解Rt△ADC,求出CD=AC•sin∠DAC≈350×0.6=210海里,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=280海里,那么渔船到的避风港D处所用时间:210÷18=11$\frac{2}{3}$小时.再解Rt△ADB,求出BD=AD•tan∠BAD≈280×2.4=672海里,那么BC=BD-CD≈672-210=462海里.设强台风移动到渔船C后面200海里时所需时间为x小时,根据追及问题的等量关系列出方程(40-18)x=462-200,解方程求出x=11$\frac{10}{11}$,由于11$\frac{2}{3}$<11$\frac{10}{11}$,所以渔船能顺利躲避本次台风的影响.
解答  解:由题意可知∠BAD=67.5°,∠CAD=36.9°,AC=350海里.
解:由题意可知∠BAD=67.5°,∠CAD=36.9°,AC=350海里.
在Rt△ADC中,∵∠ADC=90°,∠DAC=36.9°,AC=350海里,
∴CD=AC•sin∠DAC≈350×0.6=210海里,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=280海里.
∴渔船到的避风港D处所用时间:210÷18=11$\frac{2}{3}$小时.
在Rt△ADB中,∵∠ADB=90°,∠BAD=67.5°,
∴BD=AD•tan∠BAD≈280×2.4=672海里,
∴BC=BD-CD≈672-210=462海里.
设强台风移动到渔船C后面200海里时所需时间为x小时,根据题意得
(40-18)x=462-200,
解得x=11$\frac{10}{11}$,
∵11$\frac{2}{3}$<11$\frac{10}{11}$,
∴渔船能顺利躲避本次台风的影响.
点评 本题考查了解直角三角形的应用-方向角问题,难度中等,求出强台风移动到渔船C后面200海里时所需时间是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 某校男子足球队的年龄分布如图条形图所示,则这些队员年龄的众数是( )
某校男子足球队的年龄分布如图条形图所示,则这些队员年龄的众数是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
 如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |