题目内容
7.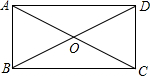 如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.
如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.
分析 由矩形的性质得出∠ADC=90°,OA=OD,由∠CDG:∠GDA=1:3,得出∠CDG=$\frac{1}{4}$×90°=22.5°,∠GDA=67.5°,求出∠ODA=22.5°,即可得出∠BDG的度数;求出OD=$\frac{1}{2}$AC=4,由三角函数即可求出DG.
解答 解:如图所示: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠ADC=90°,OA=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OD,
∴∠OAD=∠ODA,
∵∠CDG:∠GDA=1:3,
∴∠CDG=$\frac{1}{4}$×90°=22.5°,∠GDA=67.5°,
∵DG⊥AC,
∴∠OAD=∠CDG=22.5°,
∴∠ODA=22.5°,
∴∠BDG=67.5°-22.5°=45°,
故答案为:45°;
∵AC=8,
∴OD=OA=$\frac{1}{2}$AC=4,
∵∠BDG=45°,
∴DG=OD•cos45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了矩形的性质、等腰三角形的性质、三角函数;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
17.下列实数中是无理数的是( )
| A. | -$\sqrt{4}$ | B. | $\root{3}{8}$ | C. | π0 | D. | -$\frac{\sqrt{2}}{2}$ |
18.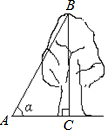 如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )| A. | 6sinα米 | B. | 6tanα米 | C. | $\frac{6}{tanα}$米 | D. | $\frac{6}{cosα}$米 |
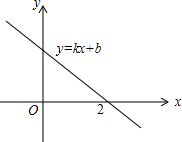 如图,一次函数y=kx+b的图象与x轴的交点为(2,0),则下列说法正确的有①②③
如图,一次函数y=kx+b的图象与x轴的交点为(2,0),则下列说法正确的有①②③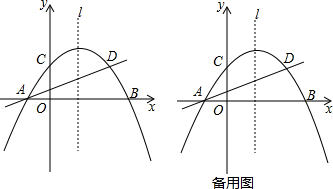
 如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).
如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).