题目内容
 如图,在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,且AB=2,EF=FG=2
如图,在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,且AB=2,EF=FG=2| 2 |
A、26+16
| ||
B、30+15
| ||
C、32+16
| ||
D、15+30
|
考点:等腰梯形的性质,矩形的性质,直角梯形
专题:
分析:作直线GF交DE的延长线于M,交直线AB于N,延长DC,交直线AB于K,从而得出四边形DMNK是矩形,△EMF、△ANG、△BKC是等腰直角三角形,进而求得矩形的面积和等腰三角形的面积,根据S七边形=S矩形-S△EMF-S△ANG-S△BKC即可求得这个七边形的面积.
解答: 解:作直线GF交DE的延长线于M,交直线AB于N,延长DC,交直线AB于K,
解:作直线GF交DE的延长线于M,交直线AB于N,延长DC,交直线AB于K,
∵在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,
∴∠A=∠B=∠C=∠E=∠F=∠G=135°,
∴∠MEF=∠MFE=45°,
∴∠M=90°,
∴ME=MF=
EF=
×2
=2,
同理可证:∠N=∠K=90°,GN=AN=BK=KC=
×4=2
,∵
∵∠M=∠N=∠K=∠D=90°,
∴四边形DMNK是矩形,
∵MN=MF+FG+GN=2+4
,NK=AN+AB+BK=2+4
,
∴S七边形=S矩形-S△EMF-S△ANG-S△BKC=MN•NK-
EM•MF-
GN•AN-
BK•CK=(2+4
)2-
×2×2-2×
×2
×2
=26+16
.
故选A.
 解:作直线GF交DE的延长线于M,交直线AB于N,延长DC,交直线AB于K,
解:作直线GF交DE的延长线于M,交直线AB于N,延长DC,交直线AB于K,∵在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,
∴∠A=∠B=∠C=∠E=∠F=∠G=135°,
∴∠MEF=∠MFE=45°,
∴∠M=90°,
∴ME=MF=
| ||
| 2 |
| ||
| 2 |
| 2 |
同理可证:∠N=∠K=90°,GN=AN=BK=KC=
| ||
| 2 |
| 2 |
∵∠M=∠N=∠K=∠D=90°,
∴四边形DMNK是矩形,
∵MN=MF+FG+GN=2+4
| 2 |
| 2 |
∴S七边形=S矩形-S△EMF-S△ANG-S△BKC=MN•NK-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故选A.
点评:本题考查了矩形的判定和性质,等腰直角三角形的判定和性质,作出辅助线构建矩形是本题的关键.

练习册系列答案
相关题目
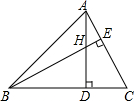 如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为
如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为 用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)
用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm) 如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折?
如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折? 如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?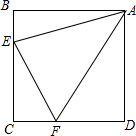 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小. 如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积.
如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积.