题目内容
8.直线y=2x-4与抛物线y=ax2有唯一公共点,求a的值.分析 根据函数图象有唯一公共点,可得判别式为零,根据解方程,可得答案.
解答 解:由y=2x-4与抛物线y=ax2有唯一公共点,得
ax2-2x+4=0.
△=b2-4ac=4-4×4a=0.
解得a=$\frac{1}{4}$,
直线y=2x-4与抛物线y=ax2有唯一公共点,a的值是$\frac{1}{4}$.
点评 本题考查了二次函数的性质,利用图象有唯一公共点得出判别式等于零是解题关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
7.某居民小区共有300户家庭,有关部门对该小区的自来水管网系统进行改进,为此需了解该小区自来水用水量的情况,该部门通过随机抽样,调查了其中20户家庭,统计了这20户家庭的月用水量,见如表:
(1)这个问题中样本是其中20户家庭自来水用水量,样本容量是20;
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.
| 月用水量(m3) | 4 | 6 | 7 | 12 | 14 | 15 |
| 户数 | 2 | 4 | 6 | 2 | 2 | 4 |
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.
16.在△ABC中,∠C=90°,AC=$2\sqrt{5}$,∠A的角平分线交BC于D,且AD=$\frac{4}{3}\sqrt{15}$,则tanB的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
20.已知反比例函数y=$\frac{k}{x}$,当x=2时,y=1,则一次函数y=kx+1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
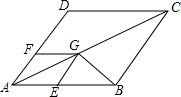 如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2.
如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2. [实际情境]
[实际情境] 如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.
如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.