题目内容
8.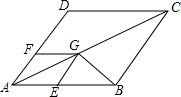 如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2.
如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2.
分析 分两种情形:①如图1中,当CB=CG时,连接BD交AC于点O,②如图2中,当GC=GB时,作GM⊥BC于M,先证明AC=$\sqrt{3}$AD,AG=$\sqrt{3}$AF,求出AG即可解决问题.
解答 解:①如图1中, 当CB=CG时,连接BD交AC于点O,
当CB=CG时,连接BD交AC于点O,
∵四边形ABCD是菱形,
∴AD=AB=3,AO=OC,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴AO=$\frac{\sqrt{3}}{2}$AD,AC=$\sqrt{3}$AD,同理AG=$\sqrt{3}$AF,
∴AC=3$\sqrt{3}$,AG=AC-CG=3$\sqrt{3}$-3,
∴3$\sqrt{3}$-3=$\sqrt{3}$AF,
∴AF=3-$\sqrt{3}$.
②如图2中, 当GC=GB时,作GM⊥BC于M,
当GC=GB时,作GM⊥BC于M,
在RT△GCM中,∵∠GMC=90°,CM=BM=$\frac{3}{2}$,∠GCM=30°
∴CG=$\frac{CM}{cos30°}$=$\frac{\frac{3}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{3}$,
∴AG=AC-CG=2$\sqrt{3}$,
∴2$\sqrt{3}$=$\sqrt{3}$AF,
∴AF=2.
故答案为3-$\sqrt{3}$或2.
点评 本题考查菱形的性质、等腰三角形的判定和性质,三角函数、勾股定理等知识,解题的关键是学会分类讨论,属于中考常考题型.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
9.下列运算结果正确的是( )
| A. | a6÷a3=a2 | B. | a3•a4=a7 | C. | (a2)3=a5 | D. | 2a3+a3=3a6 |
 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( ) 如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )
如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )



 如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.
如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.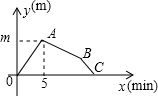 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.