题目内容
已知y2+5y+1=0,求
的值.
| y2 |
| y4-3y2+1 |
考点:分式的化简求值
专题:计算题
分析:先把y2+5y+1=0两边除以y可得y+
=-5,再利用倒数法求解:变形
得到y2-3+
,利用配方法得到(y+
)2-5,然后利用整体代入的方法可计算出值,从而可得
的值.
| 1 |
| y |
| y4-3y2+1 |
| y2 |
| 1 |
| y2 |
| 1 |
| y |
| y2 |
| y4-3y2+1 |
解答:解:∵y2+5y+1=0,
∴y+
=-5,
∴
=y2-3+
=(y+
)2-5=(-5)2-5=20,
∴
=
.
∴y+
| 1 |
| y |
∴
| y4-3y2+1 |
| y2 |
| 1 |
| y2 |
| 1 |
| y |
∴
| y2 |
| y4-3y2+1 |
| 1 |
| 20 |
点评:本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整.

练习册系列答案
相关题目
下列函数中,是y关于x的一次函数的是( )
A、y=
| ||
| B、y=2x3-1 | ||
| C、y=3-7x | ||
D、y=5-
|
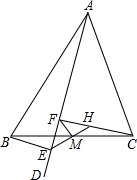 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论中:(1)M是BC的中点.(2)CF⊥AD.(3)FM⊥BC.(4)FM=
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论中:(1)M是BC的中点.(2)CF⊥AD.(3)FM⊥BC.(4)FM=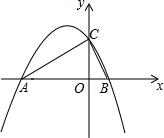 如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式.
如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式. 如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?说明理由.
如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?说明理由.