题目内容
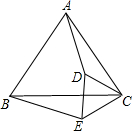
 如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?说明理由.
如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?说明理由.考点:三角形三边关系
专题:
分析:先根据三角形三边关系定理可得AD+CD>AC,BD+CD>BC,再将两式相加得(AD+BD)+2CD>AC+BC,即AB+2CD>AC+BC.
解答:解:AB+2CD>AC+BC成立,理由如下:
在三角形ADC中,AD+CD>AC,
在三角形BCD中,BD+CD>BC,
两式相加得(AD+BD)+2CD>AC+BC,
即AB+2CD>AC+BC.
在三角形ADC中,AD+CD>AC,
在三角形BCD中,BD+CD>BC,
两式相加得(AD+BD)+2CD>AC+BC,
即AB+2CD>AC+BC.
点评:本题考查了三角形三边关系定理:三角形两边之和大于第三边.同时考查了不等式的性质.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图所示,已知:△ABC和△CDE都是等边三角形,求证:AD=BE.
如图所示,已知:△ABC和△CDE都是等边三角形,求证:AD=BE. 如图,∠1=∠2,请你添加一个条件
如图,∠1=∠2,请你添加一个条件 张红和王伟为了争取到一张观看CBA联赛的入场券,他们自设计了一个方案:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘).计算张红获得入场券的概率,并说明张红的方案是否公平.
张红和王伟为了争取到一张观看CBA联赛的入场券,他们自设计了一个方案:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘).计算张红获得入场券的概率,并说明张红的方案是否公平.