题目内容
9. 如图,△ABC中,AC=BC,∠C=90°,点D为AB的中点,点E在边AC上,连接DE,过点D作DG⊥DE交BC于点G,∠EDG平分线DF交BC于F,连EF.求证:∠FED=∠AED.
如图,△ABC中,AC=BC,∠C=90°,点D为AB的中点,点E在边AC上,连接DE,过点D作DG⊥DE交BC于点G,∠EDG平分线DF交BC于F,连EF.求证:∠FED=∠AED.
分析 连接CD,根据ASA证明△AED≌△CGD,得到DE=DG,∠AED=∠FGD,再根据SAS证明△DFE≌△DFG,得到∠FED=∠FGD,即可证明∠FED=∠AED.
解答 证明:连接CD, ∵AC=BC,∠C=90°,点D为AB的中点,
∵AC=BC,∠C=90°,点D为AB的中点,
∴AD=CD=BD,∠A=∠DCG=∠ACD=∠B=45°,∠CDA=∠CDB=90°,
∵DG⊥DE,
∴∠EDG=90°,
∴∠ADE=∠CDG,
在△AED和△CGD中,
$\left\{\begin{array}{l}{∠A=∠DCG}\\{AD=CD}\\{∠ADE=∠CDG}\end{array}\right.$,
∴△AED≌△CGD(ASA),
∴DE=DG,∠AED=∠FGD,
∵∠EDG平分线DF交BC于F,
∴∠EDF=∠GDF,
在△DFE和△DFG中,
$\left\{\begin{array}{l}{DE=DG}\\{∠EDF=∠GDF}\\{DF=DF}\end{array}\right.$,
∴△DFE≌△DFG(SAS),
∴∠FED=∠FGD,
∴∠FED=∠AED.
点评 本题主要考查了全等三角形的判定与性质和等腰直角三角形的性质,熟练地掌握全等三角形的判定方法和等腰直角三角形的性质是解决问题的关键.

练习册系列答案
相关题目
1.△ABC的三边长分别为a、b、c(其中a、b、c为正数).
(1)填表:
(2)观察表格,你有什么发现?并说明理由;
(3)关于勾股数,你还有什么发现?
(1)填表:
| a | b | c | △ABC是否为直角三角形 |
| 4 | 3 | 5 | 是 |
| 6 | 8 | 10 | 是 |
| 8 | 15 | 17 | 是 |
| 10 | 24 | 26 | 是 |
| 12 | 35 | 37 | 是 |
(3)关于勾股数,你还有什么发现?
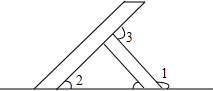 一天,爸爸带小明到建筑工地玩,他们看到一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于140°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是40°.
一天,爸爸带小明到建筑工地玩,他们看到一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于140°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是40°. 如图,在⊙O中,ON⊥CD,OM⊥AB,ON=3cm,OA=5cm,AB=8cm,求OM及CD的长.
如图,在⊙O中,ON⊥CD,OM⊥AB,ON=3cm,OA=5cm,AB=8cm,求OM及CD的长. 如图,在⊙O中,AB、BC为弦,OC与AB相交于点D,试探索∠OBD、∠DCB、∠ODB之间的数量关系.
如图,在⊙O中,AB、BC为弦,OC与AB相交于点D,试探索∠OBD、∠DCB、∠ODB之间的数量关系.