题目内容
 如图,直线AB与CD相交于点O,∠AOM=90°.
如图,直线AB与CD相交于点O,∠AOM=90°.(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据角平分线的定义求出∠AOC=45°,然后根据邻补角的定义求解即可;
(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON=
∠CON,再根据∠BOM列出方程求解x,然后求解即可.
(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON=
| 1 |
| 2 |
解答:解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=
∠AOM=
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
∠CON=
x°,
∵∠BOM=
x+x=90°,
∴x=36°,
∴∠MON=
x°=
×36°=54°,
即∠MON的度数为54°.
∴∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠BOM=
| 3 |
| 2 |
∴x=36°,
∴∠MON=
| 3 |
| 2 |
| 3 |
| 2 |
即∠MON的度数为54°.
点评:本题考查了对顶角、邻补角,角平分线的定义,此类题目熟记概念并准确识图是解题的关键,(2)难点在于根据∠BOM列出方程.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知
和
是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( )
|
|
| A、y=-2x-3 | ||||
B、y=
| ||||
| C、y=-9x+3 | ||||
D、y=-
|
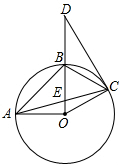 如图,已知⊙O上A、B、C三点,∠BAC=∠BCD,D是OB延长线上的点,∠BDC=30°,⊙O半径为2,AO⊥BO,BO与AC交于点E.
如图,已知⊙O上A、B、C三点,∠BAC=∠BCD,D是OB延长线上的点,∠BDC=30°,⊙O半径为2,AO⊥BO,BO与AC交于点E.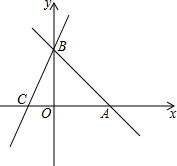 直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1. 如图,直线AB、CD相交于点O,EO⊥CD,∠AOE=68°,则∠BOD=
如图,直线AB、CD相交于点O,EO⊥CD,∠AOE=68°,则∠BOD=