题目内容
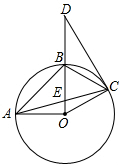 如图,已知⊙O上A、B、C三点,∠BAC=∠BCD,D是OB延长线上的点,∠BDC=30°,⊙O半径为2,AO⊥BO,BO与AC交于点E.
如图,已知⊙O上A、B、C三点,∠BAC=∠BCD,D是OB延长线上的点,∠BDC=30°,⊙O半径为2,AO⊥BO,BO与AC交于点E.(1)求证:CD是⊙O的切线;
(2)求证:AB2=AE•AC;
(3)求AC:AE的值.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)根据圆周角定理得∠BAC=
∠BOC,加上∠BAC=∠BCD,则∠BCD=
∠BOC,再利用等腰三角形的性质和三角形内角和定理可计算出∠OCB=∠OBC=90°-
∠BOC,则∠OCB+∠BCD=90°,即∠OCD=90°,于是根据切线的判定定理即可得到CD是⊙O的切线;
(2)由AO⊥BO得∠AOB=90°,根据圆周角定理得∠ACB=
∠AOB=45°,再证明△AOB为等腰直角三角形得到∠ABO=45°,则可判断△ABE∽△ACB,利用相似比可比例的性质即可得到结论;
(3)作BH⊥AC于H,如图,先利用互余计算出∠COD=60°,则可判断△BOC为等边三角形,则BC=OC=2,利用∠BCH=45°可得CH=BH=
BC=
,利用∠BAC=
∠BOC=30°可得AB=2BH=2
,AH=
BH=
,所以AC=AH+CH=
+
,然后根据AB2=AE•AC可计算出AE,再计算AC:AE的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由AO⊥BO得∠AOB=90°,根据圆周角定理得∠ACB=
| 1 |
| 2 |
(3)作BH⊥AC于H,如图,先利用互余计算出∠COD=60°,则可判断△BOC为等边三角形,则BC=OC=2,利用∠BCH=45°可得CH=BH=
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
| 6 |
| 2 |
解答:(1)证明:∵∠BAC=
∠BOC,∠BAC=∠BCD,
∴∠BCD=
∠BOC,
∵OB=OC,
∴∠OCB=∠OBC=
(180°-∠BOC)=90°-
∠BOC,
∴∠OCB+∠BCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)证明:∵AO⊥BO,
∴∠AOB=90°,
∴∠ACB=
∠AOB=45°,
∵OA=OB,
∴△AOB为等腰直角三角形,
∴∠ABO=45°,
∴∠ABO=∠ACB,
而∠BAE=∠CAB,
∴△ABE∽△ACB,
∴AB:AC=AE:AB,
∴AB2=AE•AC;
(3)解:作BH⊥AC于H,如图,
∵∠BDC=30°,∠OCD=90°,
∴∠COD=60°,
∴△BOC为等边三角形,
∴BC=OC=2,
∵∠BCH=45°,
∴CH=BH=
BC=
,
∵∠BAC=
∠BOC=30°,
∴AB=2BH=2
,AH=
BH=
,
∴AC=AH+CH=
+
,
∵AB2=AE•AC,
∴(2
)2=AE•(
+
),解得AE=2
-2
,
∴AC:AE=(
+
):(2
-2
)=(2+
):2.
| 1 |
| 2 |
∴∠BCD=
| 1 |
| 2 |
∵OB=OC,
∴∠OCB=∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OCB+∠BCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)证明:∵AO⊥BO,
∴∠AOB=90°,
∴∠ACB=
| 1 |
| 2 |
∵OA=OB,
∴△AOB为等腰直角三角形,
∴∠ABO=45°,
∴∠ABO=∠ACB,
而∠BAE=∠CAB,
∴△ABE∽△ACB,

∴AB:AC=AE:AB,
∴AB2=AE•AC;
(3)解:作BH⊥AC于H,如图,
∵∠BDC=30°,∠OCD=90°,
∴∠COD=60°,
∴△BOC为等边三角形,
∴BC=OC=2,
∵∠BCH=45°,
∴CH=BH=
| ||
| 2 |
| 2 |
∵∠BAC=
| 1 |
| 2 |
∴AB=2BH=2
| 2 |
| 3 |
| 6 |
∴AC=AH+CH=
| 6 |
| 2 |
∵AB2=AE•AC,
∴(2
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
∴AC:AE=(
| 6 |
| 2 |
| 6 |
| 2 |
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
去括号a2-2(ab-b2)-b2的值是( )
| A、a2-2ab |
| B、a2-2ab-3b2 |
| C、a2-2ab+b2 |
| D、a2-2ab+2b2 |
某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最低气温比最高气温低( )
| A、-10℃ | B、-6℃ |
| C、6℃ | D、10℃ |
平面上有三个点A,B,C,如果AB=8,AC=5,BC=3,则( )
| A、点C在线段AB上 |
| B、点C在线段AB的延长线上 |
| C、点C在直线AB外 |
| D、不能确定 |
下列结论错误的是( )
| A、若ac=bc,则a=b |
| B、若a+c=b+c,则a=b |
| C、若a=b,则a+c=b+c |
| D、若a=b,则ac=bc |
 如图,点P是第二象限内的一点,且在反比例函数y=
如图,点P是第二象限内的一点,且在反比例函数y=| k |
| x |
| A、3 | B、-3 | C、6 | D、-6 |
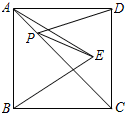 如图所示,正方形ABCD内作△ABE是等边三角形,在对角线AC上有一点P,使PD+PE的和最小为5,则这个正方形ABCD的面积为
如图所示,正方形ABCD内作△ABE是等边三角形,在对角线AC上有一点P,使PD+PE的和最小为5,则这个正方形ABCD的面积为 如图,直线AB与CD相交于点O,∠AOM=90°.
如图,直线AB与CD相交于点O,∠AOM=90°.