题目内容
14.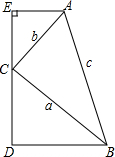 如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.
如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.(1)判断△ABC的形状;
(2)若C为ED中点,求证:ED2=4AE•BD.
分析 (1)根据已知条件得到△=(-2b)2-4(a+c)(a-c)=4(b2-a2+c2)=0,求得b2+c2=a2,于是得到结论;
(2)根据余角的性质得到∠EAC=∠BCD,推出△ACE∽△BDC,得到比例式$\frac{AE}{CD}=\frac{CE}{BD}$,根据线段中点的定义得到CE=CD=$\frac{1}{2}$DE,等量代换即可得到结论.
解答 解:(1)方程(a+c)x2-2bx-a+c=0有两相等实根.
∴△=(-2b)2-4(a+c)(a-c)=4(b2-a2+c2)=0,
∴b2+c2=a2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,
∴∠ACB=90°,
∵∠E=90°,AE∥BD,
∴∠D=∠E=90°,
∴∠ACE+∠EAC=∠ACE+∠BCD=90°,
∴∠EAC=∠BCD,
∴△ACE∽△BDC,
∴$\frac{AE}{CD}=\frac{CE}{BD}$,
∵C为ED中点,
∴CE=CD=$\frac{1}{2}$DE,
∴CD•CE=AE•BD,
∴ED2=4AE•BD.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,一元二次方程根与系数的关系,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B. △ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )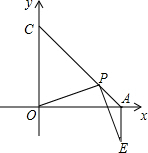 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.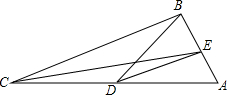 如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.
如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.