题目内容
1.已知有理数a,b,c满足|a-1|+|a+b|+|a+b+c-2|=0,则代数式(-3ab)•(-a2c)•6ab2的值为-36.分析 首先由非负数的性质可求得a、b、c的值,然后再将a、b、c的值计算即可.
解答 解:∵|a-1|+|a+b|+|a+b+c-2|=0,
∴a-1=0,a+b=0,a+b+c-2=0.
∴a=1,b=-1,c=2.
将a=1,b=-1,c=2,代入得:原式=-3×1×(-1)×[-(-1)2×2]×6×1×(-1)2=3×(-2)×6=-36.
故答案为:-36.
点评 本题主要考查的是非负数的性质、求代数式的值、有理数的混合运算,由非负数的性质可求得a、b、c的值是解题的关键.

练习册系列答案
相关题目
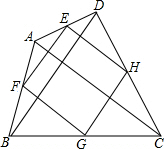 如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:
如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:



 如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.
如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.