题目内容
13.抛物线y=x2+bx+c经过点A(1,0),B(-1,1),求抛物线的解析式和顶点坐标.分析 利用待定系数法即可求出二次函数解析式,化为顶点式即可求出抛物线的顶点坐标.
解答 解:把点A(1,0),B(-1,1)代入y=-x2+bx+c,得
$\left\{\begin{array}{l}{1+b+c=0}\\{1-b+c=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{1}{2}}\\{c=-\frac{1}{2}}\end{array}\right.$,
所以抛物线的解析式为y=x2-$\frac{1}{2}$x-$\frac{1}{2}$.
y=x2-$\frac{1}{2}$x-$\frac{1}{2}$=(x-$\frac{1}{4}$)2-$\frac{9}{16}$,所以抛物线的顶点坐标为($\frac{1}{4}$,-$\frac{9}{16}$).
点评 本题主要考查了用待定系数法求二次函数解析式及二次函数的性质,解题的关键是正确求出二次函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
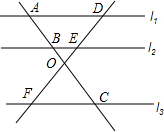 已知:l1∥l2∥l3,
已知:l1∥l2∥l3, 如图,在?ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
如图,在?ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.