题目内容
1. 如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 30 |
分析 由?ABCD的对角线AC和BD交于点O,若AC=10,BD=6,AD=4,易求得OA与OB的长,又由勾股定理的逆定理,证得AD⊥BD,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,且AC=10,BD=6,
∴OA=OC=$\frac{1}{2}$AC=5,OB=OD=$\frac{1}{2}$BD=3,
∵AD=4,
∴AD2+DO2=OA2,
∴△ADO是直角三角形,且∠BDA=90°,
即AD⊥BD,
∴?ABCD面积为:AD•BD=4×6=24.
故选C.
点评 此题考查了平行四边形的性质与勾股定理的逆定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
12.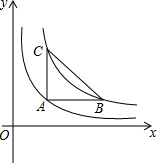 已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
 已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )| A. | $\frac{a-b}{2}$ | B. | $\frac{(a-b)^{2}}{2}$ | C. | $\frac{(a-b)^{2}}{2a}$ | D. | $\frac{(a-b)^{2}}{2b}$ |
16.不等式组$\left\{\begin{array}{l}{x<-2}\\{x>-3}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x<-2 | C. | -3<x<-2 | D. | 无解 |
6.已知(x+m)2=x2+nx+36,则n的值为( )
| A. | ±6 | B. | ±12 | C. | ±18 | D. | ±72 |
10.下列计算正确的是( )
| A. | x3•x2=x5 | B. | x5÷x=x3 | C. | (x2)3=x5 | D. | (3x)2=6x2 |
11. 滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:
滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:
(1)请你把下面的表格填写完整:
(2)考虑平均数与方差,你认为哪个年级的团体成绩更好些;
(3)假设在每个年级的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
 滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:
滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:(1)请你把下面的表格填写完整:
| 成绩统计 | 众数 | 平均数 | 方差 |
| 七年级 | 80 | 85.7 | 39.61 |
| 八年级 | 85 | 85.7 | 27.81 |
(3)假设在每个年级的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
 如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.
如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.