Question

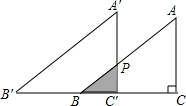如图，△ABC≌A′B′C′，∠C=∠C′=90°，AC=3cm，A′B′=5cm，先将△ABC和△A′B′C′完全重合，再将△ABC固定，△A′B′C′沿CB所在的直线向左以每秒1cm的速度平行移动，设移动x秒后，△ABC与△A′B′C′的重叠部分的面积为ycm²，求：
（1）则y与x之间的函数关系式；
（2）多少秒后重叠部分的面积为

3

8

cm²．

Answer 1

考点：一元二次方程的应用,根据实际问题列二次函数关系式,平移的性质

专题：几何动点问题

分析：（1）利用相似三角形的判定与性质表示出PC′的长，再利用三角形面积求法得出即可；
（2）利用（1）中所求关系式进而代入求出即可．

解答：解：（1）设移动xs后，△A′B′C′与△ABC的重合部分的面积为ycm²，
则此时CC′=xcm，BC′=（4-x）cm，
∵PC′∥AC，
∴△BPC′∽△BAC，
∴

B′C′

BC

=

PC′

AC

，
∴

4-x

4

=

PC′

3

=，
解得：PC′=3-

3

4

x，
故y=

1

2

×PC′×BC′=

1

2

×（3-

3

4

x）×（4-x）=

3

8

x²-3x+6；

（2）当

3

8

=

3

8

x²-3x+7，
解得：x₁=3，x₂=5（不合题意舍去），
答：3秒后两个三角形重合部分的面积等于

3

8

cm²．

点评：此题主要考查了一元二次方程的应用以及相似三角形的判定与性质，得出△BPC′∽△BAC是解题关键．