题目内容
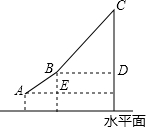 如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)
如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)考点:解直角三角形的应用
专题:
分析:先根据题意得到BE,CD的长,在Rt△ABE中,由三角函数可得AB的长度,在Rt△BCD中,由三角函数可得BC的长度,再相加即可得到答案.
解答:解:BE=400-130=270(米),
CD=1000-400=600(米),
在Rt△ABE中,AB=
=540(米),
在Rt△BCD中,BC=
=600
≈848(米),
AB+BC=540+848=1388(米).
答:钢缆AB和BC的总长度大约是1388米.
CD=1000-400=600(米),
在Rt△ABE中,AB=
| BE |
| sin30° |
在Rt△BCD中,BC=
| CD |
| sin45° |
| 2 |
AB+BC=540+848=1388(米).
答:钢缆AB和BC的总长度大约是1388米.
点评:此题考查了解直角三角形的应用,关键是根据三角函数得到AB和BC的长度.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,Rt△ABC绕点C顺时针旋转90°得Rt△EDC,连结AE,则AE的大小是( )
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,Rt△ABC绕点C顺时针旋转90°得Rt△EDC,连结AE,则AE的大小是( )
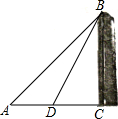 津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(
津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB( 已知:如图,点A,C,D,B在同一条直线上,AC=BD,AE=BF,∠A=∠B.求证:∠E=∠F.
已知:如图,点A,C,D,B在同一条直线上,AC=BD,AE=BF,∠A=∠B.求证:∠E=∠F. 如图,在△ABC中,AB=AC,∠CAB=30°.
如图,在△ABC中,AB=AC,∠CAB=30°. △ABC在直角坐标系内的位置如图.
△ABC在直角坐标系内的位置如图.