题目内容
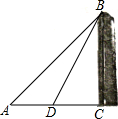 津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(
津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先津塔的高度CB=xm,由题意即可求得BC=AC=xm,然后根据∠BDC的正切求得BC的长即可.
解答:解:设津塔的高度CB=xm,
由题意可知∠C=90°,
∵∠A=45°,
∴AC=BC=xm,
∵AD=142.6m,
∴CD=x-142.6m,
在Rt△BDC中,
∵∠BDC=60°,
∴tan60°=
=
,
即
=
,
∴x=337.2m,
答:津塔的高度CB约为337.2m.
由题意可知∠C=90°,
∵∠A=45°,
∴AC=BC=xm,
∵AD=142.6m,
∴CD=x-142.6m,
在Rt△BDC中,
∵∠BDC=60°,
∴tan60°=
| BC |
| DC |
| 3 |
即
| x |
| x-142.6 |
| 3 |
∴x=337.2m,
答:津塔的高度CB约为337.2m.
点评:本题考查了解直角三角形的应用-仰角俯角,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
如图是一个物体的三视图,则此三视图所描述物体的直观图是( )


A、 |
B、 |
C、 |
D、 |
 已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.
已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.
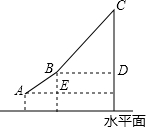 如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)
如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m) 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题: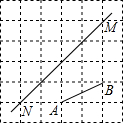 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.